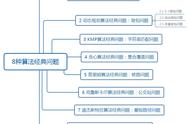
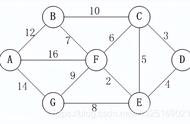
Step2,在所有边中找出长度最短的一条,即AB=3。

Step3,在剩余的边中继续找长度最短的边,此时AD、CD、EF都是4,观察可知A、C、D、E、F都在不同的连同分量上,所以把这三条边加入进来。

Step4,在剩余的边中继续找长度最短的边,即BE=5,观察可知B、E分属两个不同的连同分量,所以把BE加进来。

搞定!结果跟普利姆算法一模一样!不用说也知道,这便是最优解。
游戏中修路如此,实际生活中的很多问题也如出一辙,例如城市之间铺设光缆,轨道建设,工程布网等,实际上都可以抽象成最小生成树问题。掌握以上两种算法,此类问题便迎刃立解。
张大少友情提醒:两种算法功能等效,但适用条件有所不同。因为二者的时间复杂度不同。普利姆算法适用于求解边稠密而顶点不多的场合;而克鲁斯卡尔算法适用于求解边稀疏的场合。若要深入了解,请老少爷们参考相关的算法教程,在下不再赘述。
青山不改,绿水长流,在下告退。
转发随意,转载请联系张大少本尊。