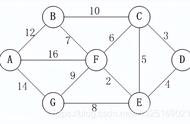
普里姆(Prim)算法最小生成树一般有Prim算法和Dijkstra算法。小编就详细的介绍这两种算法。
Prim算法是用于生成无向带权连通图的最小生成树(MST)的一种算法, 并且可以解决边权值为负的情况. Prim算法从任意一顶点x开始, 初始化V'=x, 每次采取贪心策略选取跨越V与V-V'的最小边, 扩大现有的子树V', 直到遍历了图中所有的顶点.
算法流程
从以上分析可以知道, Prim算法与Dijkstra算法的求解思路一致, 但是在Dijkstra算法中, dist数组维护了当前顶点到源点node的最短距离; 而在Prim算法中, dist维护了当前顶点到当前生成树的距离.
1. 初始化dist数组为INF, 访问数组vis为false.
2.选定任意一个节点node, 标记vis[node]=true, dist[node]=0
3. 找出所有未访问过的点中的距离最小的点u, 标记vis[u]=true, 将最后一次松弛的边加入生成树
4. 以u作为中间点, 访问其所有邻边进行松弛, 被松弛的点v记录下(u,v)边
5. 循环|V|-1次
算法模板:
void prim() {
memset(vis,0x00,sizeof vis);
for(int i = 1; i <= n; i) {
dist[i] = INF;
}
dist[1] = 0;
int ans = 0;
for(int i = 1; i <= n; i) {
int node = -1;
for(int j = 1; j <= n; j) {
if(!vis[j] && (node == -1 || dist[j] > dist[node])) {
node = j;
}
if(node==-1) break;
vis[node] = true;
ans = dist[node];
for (int j = 1; j <= n; j) {
dist[j] = min(dist[j], g[node][j]);
}
}
}
}
时间复杂度
Prim算法循环|V|-1次, 使用线性扫描算法寻找最小值的时间复杂度为O(|V|^2 |E|), 使用堆优化版Prim算法的时间复杂度是O(|E|log|V|).
克鲁斯卡尔(Kruskal)算法算法流程:
- 将图G中每个顶点看做独立的连通分量.
- 将所有边按照权值从小到大排序加入集合S
- 从S中取出一条权值最小的边(u, v), 如果u和v不在同一个连通分量中, 合并u和v所在的连通分量, 同时将(u, v)加入生成树的边集合E'
- 重复(3)直到所有节点在一个连通分量中, 边集合E'就是MST.
算法模板:
public class prim {
static int N = 9; // 图中边的数量
static int P = 6; // 图中顶点的数量
//构建表示路径的类
public static class edge implements Comparable<edge>{
//每个路径都有 2 个顶点和 1 个权值
int initial;
int end;
int weight;
public edge(int initial, int end, int weight) {
this.initial = initial;
this.end = end;
this.weight = weight;
}
//对每个 edge 对象根据权值做升序排序
@Override
public int compareTo(edge o) {
return this.weight - o.weight;
}
}
public static void kruskal_MinTree(edge[] edges,edge [] minTree) {
int []assists = new int[P];
//每个顶点配置一个不同的标记值
for (int i = 0; i < P; i ) {
assists[i] = i;
}
//根据权值,对所有边进行升序排序
Arrays.sort(edges);
//遍历所有的边
int num = 0;
for (int i = 0; i < N; i ) {
//找到当前边的两个顶点在 assists 数组中的位置下标
int initial = edges[i].initial - 1;
int end = edges[i].end - 1;
//如果顶点位置存在且顶点的标记不同,说明不在一个集合中,不会产生回路
if (assists[initial] != assists[end]) {
//记录该边,作为最小生成树的组成部分
minTree[num] = edges[i];
//计数 1
num ;
int elem = assists[end];
//将新加入生成树的顶点标记全不更改为一样的
for (int k = 0; k < P; k ) {
if (assists[k] == elem) {
assists[k] = assists[initial];
}
}
//如果选择的边的数量和顶点数相差1,证明最小生成树已经形成,退出循环
if (num == P - 1) {
break;
}
}
}
}
public static void display(edge [] minTree) {
System.out.println("最小生成树为:");
int cost = 0;
for (int i = 0; i < P - 1; i ) {
System.out.println(minTree[i].initial " - " minTree[i].end " 权值为:" minTree[i].weight);
cost = minTree[i].weight;
}
System.out.print("总权值为:" cost);
}
public static void main(String[] args) {
Scanner scn = new Scanner(System.in);
edge[] edges = new edge[N];
edge[] minTree = new edge[P-1];
System.out.println("请输入图中各个边的信息:");
for(int i=0;i<N;i ) {
int initial = scn.nextInt(), end = scn.nextInt(), weight = scn.nextInt();
edges[i] = new edge(initial,end,weight);
}
kruskal_MinTree(edges,minTree);
display(minTree);
}
}总结
稀疏图一般选择 prim,采用 邻接矩阵 进行存储边之间的关系。
稠密图一般选择 Kruskal ,采用邻接表进行存储边之间的关系(更多采用结构体的方式)。