最小生成树算法:普里姆算法与克鲁斯卡尔算法的探索
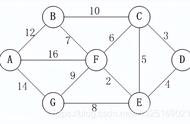
在图论中,最小生成树问题是一个核心而有趣的研究领域。最小生成树是指在一个加权连通图中,包含所有顶点的树形子图,且所有边的权值之和最小。普里姆算法和克鲁斯卡尔算法是求解最小生成树的两种经典算法,它们各自具有独特的实现方式和应用场景。

首先,我们来看看普里姆算法。普里姆算法是一种贪心算法,它的基本思想是从一个顶点开始,每次选择与当前生成树距离最短的顶点加入生成树中,直到所有顶点都被包括在内。在实现上,我们通常使用邻接矩阵或邻接表来表示图,并利用一个数组来记录每个顶点到当前生成树的最短距离。普里姆算法的时间复杂度主要取决于图的表示方式和所使用的数据结构,通常可以在O(n^2)或O(mlogn)的时间复杂度内完成。普里姆算法的优点是简单易实现,特别适用于稠密图。然而,对于稀疏图,其性能可能不如克鲁斯卡尔算法。

接下来,我们探讨克鲁斯卡尔算法。克鲁斯卡尔算法是一种基于并查集的算法,它的基本思想是按照边的权值从小到大排序,然后依次选择权值最小的边,如果这条边连接的两个顶点不在同一个连通分量中,则将其加入最小生成树中。在实现上,我们需要使用一种数据结构来维护图的连通性,如并查集。克鲁斯卡尔算法的时间复杂度主要取决于边的数量和排序算法的选择,通常可以在O(mlogn)的时间复杂度内完成。克鲁斯卡尔算法的优点是适用于稀疏图,因为它只需要考虑边而不需要考虑顶点之间的直接关系。然而,对于稠密图,其性能可能不如普里姆算法。

在实际应用中,我们可以根据图的特性和需求选择合适的算法。对于稠密图,普里姆算法可能更为合适;而对于稀疏图,克鲁斯卡尔算法可能更为高效。此外,我们还需要考虑算法的实现难度、空间复杂度等因素。
总的来说,普里姆算法和克鲁斯卡尔算法是求解最小生成树的两种经典方法,它们各具特色,各有优势。通过深入研究这两种算法,我们可以更好地理解图论中的最小生成树问题,为实际应用提供有力的支持。同时,这两种算法也为我们提供了解决其他图论问题的思路和启示,推动了图论领域的发展。
,