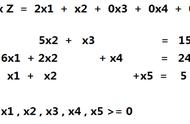此账号为华为云开发者社区官方运营账号,提供全面深入的云计算前景分析、丰富的技术干货、程序样例,分享华为云前沿资讯动态
本文分享自华为云社区《对偶理论与对偶单纯性法》,原文作者:井冈山_阳春 。
线性规划(Linear Programming,简称LP)是运筹学中研究较早、发展较快、应用广泛、方法较为成熟的一个重要分支,它是辅助人们进行科学管理的一种数学方法。对偶理论(Duality theory)就是研究线性规划中原始问题与对偶问题之间关系的理论。
1. 对偶问题的提出对偶是对同一问题,从两种不同角度观察,有两种拟似对立的表述。例如“矩形面积与周长的关系”有如下两种表述:
- 周长一定,面积最大的矩形是正方形;
- 面积一定,周长最短的矩形是正方形。
再比如,生产计划问题,如图一所示,某工厂要生产两种产品I和II,生产原料分别是A和B,且对总的生产设备台时也有限制

那么,分别生产多少件产品I和II,才能使生产的利益最大化,很显然,从卖家的角度,利用线性规划,得到的优化模型M1:

其中x1和x2分别是计划生产产品I和II的件数。换一个角度,从买家的角度,不买产品二是直接买生产原料,从盈利的角度出发假设每件生产原料的价格跟别是y1、y2和y3,买家希望购买的成本是最小的,于是有了下面的优化模型M2:

以上是两个说明对偶问题的例子。下面直接给出原问题和对偶问题的对应关系表: