一、引言
函数是数学中的重要概念,而函数的表示法则是描述和研究函数的重要手段。掌握函数的表示法对于理解函数的性质、解决数学问题以及在实际生活中的应用具有重要意义。本文将详细解析函数的三种主要表示法:解析法、图象法和表格法,帮助同学们更好地理解和运用这一知识点。

二、解析法
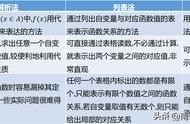
- 定义:解析法是通过数学表达式来表示函数关系的方法。它用含有数学符号和运算符号的式子来描述函数,具有精确、简洁的特点。
- 优点:解析法能够准确地反映函数的性质和行为特点,便于进行数学分析和计算。同时,解析式易于记忆和传播,方便学习和交流。
- 缺点:解析法有时难以直观地展现函数的形态和变化趋势,需要结合其他方法(如图象法)进行辅助理解。
- 应用:解析法在解决数学问题中广泛应用,如求函数的值、研究函数的性质、证明数学定理等。
三、图象法
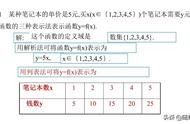
- 定义:图象法是通过在坐标系中描点、连线来表示函数关系的方法。它将函数的自变量和因变量之间的关系直观地展现在平面上,形象生动。
- 优点:图象法能够直观地展现函数的形态和变化趋势,有助于理解函数的性质和特点。同时,通过观察图象可以发现函数的一些重要性质和规律。
- 缺点:图象法难以精确地表达函数的数值关系,而且在处理复杂函数时可能会遇到困难。此外,绘制函数图象需要一定的绘图技能和经验。
- 应用:图象法在解决数学问题、分析函数性质以及进行数学实验等方面都有广泛应用。例如,通过观察函数图象可以判断函数的单调性、奇偶性等性质;通过比较不同函数的图象可以研究它们之间的关系和差异。
四、表格法
- 定义:表格法是通过列出函数自变量和对应因变量的数值表来表示函数关系的方法。它将函数的数值关系以表格的形式呈现出来,清晰明了。
- 优点:表格法能够直观地展示函数在一定范围内的数值变化情况,便于观察和比较。同时,表格法易于理解和操作,适合初学者使用。
- 缺点:表格法只能提供有限的数据点,难以全面反映函数的性质和行为特点。此外,在处理复杂函数或需要大量数据点时可能会显得繁琐和不便。
- 应用:表格法在解决一些实际问题时具有实用价值,如统计分析、经济预测等领域。同时,在学习和研究函数时,表格法可以作为其他表示法的补充和辅助手段。
五、总结与展望
通过本文的学习,同学们对“函数的表示法”这一知识点有了更深入的理解。掌握这一知识点不仅有助于提高学生的数学素养和解决问题的能力,还为后续的学习和应用奠定了坚实的基础。希望同学们在未来的学习中不断巩固和应用这一知识点,探索更多与之相关的有趣性质和应用实例。同时,也期待教育工作者和研究者们能够不断完善和拓展这一领域的教学内容和方法,为学生提供更加优质的教育资源和指导。通过不断地学习和实践,我们相信同学们一定能够熟练掌握这一知识点,并在实际生活中加以应用。
六、附加知识点与拓展
在掌握基本的函数表示法后,同学们还可以进一步学习和探索以下相关知识点和拓展内容:
- 复合函数的表示法:复合函数是由两个或两个以上的基本函数通过复合运算形成的函数。掌握复合函数的表示法有助于理解和分析更复杂的函数关系。
- 分段函数的表示法:分段函数是在其定义域的不同区间上由不同的数学表达式表示的函数。学习分段函数的表示法有助于处理一些具有特殊性质的函数问题。
- 隐函数的表示法:隐函数是一种不能直接解出因变量的函数关系,需要通过其他方式(如微分法)来研究其性质和行为特点。了解隐函数的表示法有助于拓宽对函数概念的理解和应用范围。
- 函数图像的变换与性质:通过研究函数图像的平移、伸缩、对称等变换以及图像的连续性、可导性等性质,可以更加深入地理解函数的本质和特点。这对于提高数学素养和解决问题的能力具有重要意义。