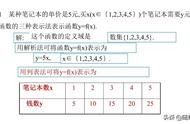
一、待定系数法求函数解析式
已知函数的类型求函数解析式,常采用待定系数法,由题设条件求待定系数。
待定系数法求函数解析式的步骤如下:
(1)设出所求函数含有待定系数的解析式;
(2)把已知条件代入解析式,列出关于待定系数的方程或方程组;
(3)解方程或方程组,得到待定系数的值;
(4)将所求待定系数的值代回所设解析式。

二、换元法、配凑法求函数解析式
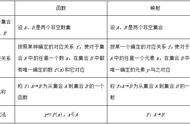
已知f(g(x))=h(x),求f(x),有两种方法:
(1)换元法,即令t=g(x),解出x,代入h(x)中,得到一个含t的解析式,再用×替换,便得到f(x)的解析式。利用换元法解题时,换元后要确定新元的取值范围,即函数 f(x)的定义域;
(2)配凑法,即在f(g(x))的解析式中配凑出“g(x)”,用含g(x)的式子来表示h(x),然后将解析式中的g(x)用x代替即可。


三、消元法(或解方程组法)求函数解析式
在已知式子中,含有关于两个不同变量的函数,而这两个变量有着某种关系,这时就要依据两个变量的关系,建立一个新的关于这两个变量的式子,由两个式子建立方程组,通过解方程组消去一个变量,得到目标变量的解析式,这种方法叫做消元法(或解方程组法)。即已知f(x)与f(の ( x ))满足的关系式,要求 f ( x )时,可用の( x )代替两边的所有的x,得到关于 f(x)与f (の( x ))的方程组,解之即可求出f(x)。

四、赋值法求函数解析式
当所给的函数中含有两个变量时,可对这两个变量交替用特殊值代入,或使这两个变量相等代入,再根据已知条件求出函数解析式。具体取什么特殊值,要据题目特征而定。