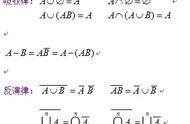这两者的区别就在于原因和结果颠倒了,而之所以可以颠倒的原因就在于P(AB)=P(BA),导致:

(2)一维随机变量及其分布
这一章的关键就是正态分布曲线:

对于曲线上的每一点(x,y),其横坐标代表的数值,纵坐标代表的是比例,比如,这条曲线如果表示一个100人的班级的考试成绩,那么横坐标就是分数,纵坐标就是这个分数的学生所占比例。这条曲线从左到右所包围的面积,就是某个分数段(比如0-60)分的学生所占的比例。这条曲线的最高点就是这个班的平均分。这条曲线还表示了一个意思,就是平均分旁边的分数的学生所在比例更高,往两边比例逐渐缩小。
(3)二维随机变量及其分布
这一章的重点应该把握边缘概率密度的概念。
一维概率密度函数f(x)指的是在x固定的情况下,x的这个值的取值频度。
同样,边缘概率密度也是一样的意思:

前者是指x固定,y在整个定义域内变动,后者则反过来。
(4)随机变量的数字特征
这一章的数学期望很简单,就是样本容量N趋于无穷大时平均值的极限值。
方差按照其公式