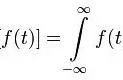傅里叶变换公式怎么用,傅里叶变换最通俗的理解 公式

，并用快速傅里叶变换（fft）检查它是否正确。

import matplotlib.pyplot as plt y_real = y[:, :signal_length] y_imag = y[:, signal_length:] tvals = np.arange(signal_length).reshape([-1, 1]) freqs = np.arange(signal_length).reshape([1, -1]) arg_vals = 2 * np.pi * tvals * freqs / signal_length sinusoids = (y_real * np.cos(arg_vals) - y_imag * np.sin(arg_vals)) / signal_length reconstructed_signal = np.sum(sinusoids, axis=1) print('rmse:', np.sqrt(np.mean((x - reconstructed_signal)**2))) plt.subplot(2, 1, 1) plt.plot(x[0,:]) plt.title('Original signal') plt.subplot(2, 1, 2) plt.plot(reconstructed_signal) plt.title('Signal reconstructed from sinusoids after DFT') plt.tight_layout() plt.show()

rmse: 2.3243522568191728e-15

得到的这个微小误差值可以证明，计算的结果是我们想要的。

• 另一种方法是重构信号：

import matplotlib.pyplot as plt y_real = y[:, :signal_length] y_imag = y[:, signal_length:] tvals = np.arange(signal_length).reshape([-1, 1]) freqs = np.arange(signal_length).reshape([1, -1]) arg_vals = 2 * np.pi * tvals * freqs / signal_length sinusoids = (y_real * np.cos(arg_vals) - y_imag * np.sin(arg_vals)) / signal_length reconstructed_signal = np.sum(sinusoids, axis=1) print('rmse:', np.sqrt(np.mean((x - reconstructed_signal)**2))) plt.subplot(2, 1, 1) plt.plot(x[0,:]) plt.title('Original signal') plt.subplot(2, 1, 2) plt.plot(reconstructed_signal) plt.title('Signal reconstructed from sinusoids after DFT') plt.tight_layout() plt.show()

rmse: 2.3243522568191728e-15

最后可以看到，DFT后从正弦信号重建的信号和原始信号能够很好地重合。

现在就到了让神经网络真正来学习的部分，这一步就不需要向之前那样预先计算权重值了。

首先，要用FFT来训练神经网络学习离散傅里叶变换：

import tensorflow as tf signal_length = 32 # Initialise weight vector to train: W_learned = tf.Variable(np.random.random([signal_length, 2 * signal_length]) - 0.5) # Expected weights, for comparison: W_expected = create_fourier_weights(signal_length) losses = [] rmses = [] for i in range(1000): # Generate a random signal each iteration: x = np.random.random([1, signal_length]) - 0.5 # Compute the expected result using the FFT: fft = np.fft.fft(x) y_true = np.hstack([fft.real, fft.imag]) with tf.GradientTape() as tape: y_pred = tf.matmul(x, W_learned) loss = tf.reduce_sum(tf.square(y_pred - y_true)) # Train weights, via gradient descent: W_gradient = tape.gradient(loss, W_learned) W_learned = tf.Variable(W_learned - 0.1 * W_gradient) losses.append(loss) rmses.append(np.sqrt(np.mean((W_learned - W_expected)**2)))

Final loss value 1.6738563548424711e-09 Final weights' rmse value 3.1525832404710523e-06

得出结果如上，这证实了神经网络确实能够学习离散傅里叶变换。

除了用快速傅里叶变化的方法，还可以通过网络来重建输入信号来学习DFT。(类似于autoencoders自编码器)。

自编码器（autoencoder, AE）是一类在半监督学习和非监督学习中使用的人工神经网络（Artificial Neural Networks, ANNs），其功能是通过将输入信息作为学习目标，对输入信息进行表征学习（representation learning）。

W_learned = tf.Variable(np.random.random([signal_length, 2 * signal_length]) - 0.5) tvals = np.arange(signal_length).reshape([-1, 1]) freqs = np.arange(signal_length).reshape([1, -1]) arg_vals = 2 * np.pi * tvals * freqs / signal_length cos_vals = tf.cos(arg_vals) / signal_length sin_vals = tf.sin(arg_vals) / signal_length losses = [] rmses = [] for i in range(10000): x = np.random.random([1, signal_length]) - 0.5 with tf.GradientTape() as tape: y_pred = tf.matmul(x, W_learned) y_real = y_pred[:, 0:signal_length] y_imag = y_pred[:, signal_length:] sinusoids = y_real * cos_vals - y_imag * sin_vals reconstructed_signal = tf.reduce_sum(sinusoids, axis=1) loss = tf.reduce_sum(tf.square(x - reconstructed_signal)) W_gradient = tape.gradient(loss, W_learned) W_learned = tf.Variable(W_learned - 0.5 * W_gradient) losses.append(loss) rmses.append(np.sqrt(np.mean((W_learned - W_expected)**2)))

Final loss value 4.161919455121241e-22 Final weights' rmse value 0.20243339269590094