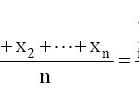在上一篇文章---"两个重要统计量——均值和比率“里,我们介绍了用样本均值`x估计未知的总体均值`a,这个`x是一个数(而不是一个范围),因此这种形式的估计叫作点估计。
另外,我们还介绍了方差和标准差,我们认识到用`x估计`a是有误差的,而标准差从平均的意义上反映了误差幅度,因此,如果我们以标准差作为衡量散布度的一个单位,把未知的总体均值`a估计在(`x -一个标准差)的范围内,这种形式的估计就叫作区间估计,因为它把未知值估计在一个范围内。
分布密度曲线与分布密度函数方差是总体中各个体指标的散布程度的综合刻画,它在一定意义上也有助于刻画样本均值在估计总体均值时的精度。但是,由于总体中个体指标值的分布可能是均匀的,可能是“两头大,中间小”或“两头小,中间大”等,这种分布上的差异,将导致区间(`x -一个标准差)的可靠程度有很大差异。
对于分布我们将做如下介绍。设一总体包含N个个体,其指标值分别为a1 , …, aN。所谓“指标值”,就是个体的某种性质的数量刻画,而这种性质是与我们所研究的问题有关的。设我们从总体中随机抽出一个个体,并以X记其指标值,常把X称为随机变量。当把相近的指标值结成一组,并给出组的比率,我们将得到如下的分布的直方图。

在许多实际问题中,总体所含个体数或者是为数极大的,或者在理论上说是无穷大的。则X这个变量原则上有无穷个可能值,我们可以采用“以有限逼近无限”的方法,在X的取值无限制地增加下,直方图在理论上愈来愈接近一条曲线,如下图(b)所示。


从理论的观点看,这条曲线给出了总体指标分布的一个完整的描述,即称为总体指标的分布密度曲线。如果在平面上引进直角坐标系,分别以x和y记一个点的横坐标和纵坐标,则一条曲线可用一个函数y=f(x)去刻画,这个f(x)也就称为总体指标的分布密度函数。