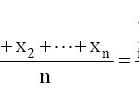区间估计的一般方法和步骤,区间估计的常用方法有矩估计法

大多数统计数据都用于估计对某个感兴趣的总体特征，比如平均家庭收入、网上购买生日礼物的人数百分比，或者美国每年消耗的冰淇淋的平均量。总体的这些特征称为参数。通常，人们希望通过从总体中抽取样本并利用样本中的统计数据来估计（做出一个很好的猜测）参数的值。问题是：如何定义“很好的估计”呢？

只要过程被正确执行，估计通常可以非常接近参数。本章将为您提供对置信区间的概述（这是统计学家使用和推荐的估计类型）；为什么应该使用它们（而不仅仅是一个数字的估计）；如何建立、计算和解释最常用的置信区间；以及如何识别误导性的估计。

阅读任何杂志、报纸或收听任何新闻广播，你会听到很多统计数据，其中许多是对某种数量的估计。您可能会想知道它们是如何得出这些统计数据的。在某些情况下，这些数字经过了深入研究；在其他情况下，它们只是瞎猜。以下是我在一本领先的商业杂志的一期中发现的一些估计的例子。它们来自各种来源：

✓ 尽管现在有些工作更难找，但一些地区确实在寻找新雇员：未来八年内，将需要13,000名麻醉护士。薪水从80,000美元到95,000美元不等。

✓ 一名大联盟棒球运动员每个赛季使用的球棒平均数量为90支。

✓ 兰博基尼从0到60英里/小时的加速时间为3.7秒，最高时速接近205英里。

这些估计有些比其他的更容易获得。以下是我对这些估计所做的一些建议：

✓ 如何估计未来八年内需要多少麻醉护士？你可以从考虑在此期间将有多少人退休开始；但这并不包括增长。对未来一两年需求的预测可能会比较接近，但八年后的未来则更难预测。

✓ 棒球运动员每个赛季使用的平均球棒数量可以通过对球员本人、照顾他们装备的人，或者为他们提供球棒的公司进行调查来找到。

✓ 确定汽车速度更困难，但可以通过使用秒表进行测试。并且应该找到相同制造和型号的许多不同汽车的平均速度，在每次相同的驾驶条件下进行测试。

并非所有的统计数据都是平等的。要确定一个统计数据是否可靠和可信，不要仅仅接受表面上的值。思考一下它是否有道理，以及您将如何制定估计。如果这个统计数据对你来说很重要，找出是什么过程用于得出这个统计数据（第16章涉及有关调查的所有元素，第17章为您提供有关实验的内幕消息）。

参数是描述一个总体的单个数字，例如美国所有家庭的家庭收入中位数。统计数据是描述样本的单个数字，例如对1200个家庭样本的家庭收入中位数。通常情况下，你不知道总体参数的值，因此你进行抽样并使用统计数据来给出你的最佳估计。

假设你想知道美国的车辆中皮卡车所占比例有多少（在这种情况下是参数）。你无法查看每辆车，因此你随机抽取了一千辆车，涵盖了不同时间和不同地点的高速公路。你发现在你的样本中，有7%的车辆是皮卡车。你不能说美国道路上所有车辆中确切有7%是皮卡车，因为你知道这只是基于你抽样的一千辆车。尽管你希望7%接近真实比例，但你不能确定，因为你的结果是基于部分车辆样本，而不是所有美国的车辆。

那么该怎么办呢？你取得的样本结果，加上和减去一些数字，以表明你正在提供总体参数的可能值范围，而不仅仅是假设样本统计等于总体参数（尽管这样做在媒体上很常见，但并不是一个好方法）。统计数据加上或从统计数据减去的这个数字称为误差边际（MOE）。加法和减法（用符号±表示）对于任何估计都有助于将结果放入透视中。当你知道误差边际时，你就能够估计如果进行另一次抽样，样本结果可能会发生多大变化。

误差边际中的误差一词并不意味着犯了错误或数据质量不好。它只是意味着样本的结果与如果你使用整个总体所得到的结果并不完全相等。这种差距是由于随机、抽样而产生的偏差，而不是由于错误。 (这就是为什么在选择样本和收集数据时最小化偏差如此重要；请参见第16章和第17章。)

一个统计数据加上或减去一个误差边际被称为置信区间：

✓ 之所以使用区间这个词，是因为你的结果变成了一个区间。例如，假设喜欢棒球的孩子的百分比是40%，加上或减去3.5%。这意味着喜欢棒球的孩子的百分比在40% – 3.5% = 36.5%和40% 3.5% = 43.5%之间。区间的下限是你的统计数据减去误差边际，上限是你的统计数据加上误差边际。

✓ 对于所有的置信区间，你对在长期内使用你的样本正确（猜测参数）有一定的信心。作为一个百分比表达，这种信心程度被称为置信水平。本章后面将为最常用的置信区间提供公式和示例。

以下是用置信区间估计参数的一般步骤。关于步骤1和步骤4-6的详细信息将在本章的其余部分介绍。步骤2和步骤3涉及抽样和数据收集，这在第16章（抽样和调查数据收集）和第17章（实验数据收集）中有详细介绍。

1. 选择你的置信水平和样本大小。
2. 从总体中随机选择一些个体组成样本。
3. 从样本中收集可靠和相关的数据。
4. 将数据汇总为一个统计数据，例如均值或比例。
5. 计算误差边际。
6. 将统计数据加上或减去误差边际，得到参数的最终估计。这一步计算了该参数的置信区间。

假设你是一名生物研究人员，试图用手抄网捕捉一条鱼，而网的大小代表着置信区间的误差边际。现在假设你的置信水平是95%。这真正意味着什么呢？这意味着如果你一遍又一遍地用这个特定的网在水中捞取，你将在95%的时间内捕到一条鱼。在这里捕到一条鱼意味着你的置信区间是正确的，并且包含了真实的参数（在这种情况下，参数由鱼本身代表）。

但这是否意味着在任何一次尝试中，你都有95%的几率捕到一条鱼？不是的。这是否令人困惑？当然是。以下是情况描述：在一次尝试中，假设你在将网浸入水中之前闭上眼睛。此时，你捕到一条鱼的机会是95%。但接着，你还是继续闭着眼睛将网在水中移动。然而，在这之后，你睁开眼睛，只能看到两种可能的结果：你要么捕到了一条鱼，要么没有；这里不再涉及概率。

同样，在数据收集完成后，并计算了置信区间之后，你要么捕捉到了真实的总体参数，要么没有。因此，你并不是说你对参数在你特定的区间内有95%的信心。你对的是随机样本被选中和创建置信区间的过程有95%的信心。也就是说，在长期内，你将在95%的时间内捕到一条鱼。

你要知道，这个过程将会在95%的情况下捕捉到总体均值的区间。在另外的5%的情况下，样本中随机收集的数据具有异常高或低的值，不能代表总体。这5%的误差只测量由于随机机会导致的误差，不包括偏差。

如果进入研究的数据是有偏的和/或不可靠的，那么误差边际是没有意义的。然而，通过查看任何人的统计结果，你无法得知这一点。我最好的建议是在接受报告的误差边际为真实之前查看数据是如何收集的（有关数据收集问题的详细信息，请参阅第16章和第17章）。这意味着在相信一项研究之前要提出问题。

你的置信区间的宽度是误差边际的两倍。例如，假设误差边际为±5%。置信区间为7%，加减5%，范围从7% – 5% = 2%一直到7% 5% = 12%。因此，置信区间的宽度为12% – 2% = 10%。一个更简单的计算方法是说置信区间的宽度是误差边际的两倍。在这种情况下，置信区间的宽度是2 * 5% = 10%。

置信区间的宽度是从区间的下限（统计值减去误差边际）到区间的上限（统计值加上误差边际）的距离。通过取两倍的误差边际，你可以快速计算置信区间的宽度。

使用置信区间进行估计的最终目标是要有一个窄的宽度，因为这意味着你正在聚焦参数是什么。不得不加上和减去一个很大的误差边际只会使你的结果不太准确。

那么，如果小的误差边际是好的，那么更小是不是更好呢？并非总是如此。一个窄的置信区间是一件好事，但是有一个限度。为了获得极窄的置信区间，你必须进行一项更大规模的、更昂贵的研究，因此有一个阶段，增加的费用无法证明在准确度上的微小差异是合理的。当估计本身是一个百分比（比如女性、共和党人或吸烟者的百分比）时，大多数人对2%到3%的误差边际都相当满意。

如何确保你的置信区间足够窄呢？在收集数据之前，你肯定要考虑这个问题；在收集数据之后，置信区间的宽度就确定了。

三个因素影响置信区间的宽度：

✓ 置信水平

✓ 样本大小

✓ 总体变异量

这三个因素各自在影响置信区间的宽度方面发挥着重要作用。在接下来的章节中，你将探讨每个元素的详细信息以及它们如何影响宽度。

每个置信区间（实际上每个误差边际）都与一个百分比相关联，代表了你对结果能否捕捉到真实的总体参数有多有信心，这取决于你的随机样本的运气。这个百分比被称为置信水平。

置信水平帮助你考虑到在仅使用一个样本的数据进行参数估计时可能得到的其他可能样本结果。如果你想考虑到其他95%的可能结果，你的置信水平就是95%。

研究人员通常使用什么置信水平？我见过的置信水平范围从80%到99%不等。最常见的置信水平是95%。事实上，统计学家有一句俗语：“为什么统计学家喜欢他们的工作？因为他们只需要在95%的时间里正确。”

样本结果的变异性以标准误差来衡量。标准误差类似于数据集的标准偏差，只是标准误差适用于样本均值或样本百分比，如果采用不同的样本，则可能得到不同的样本均值或样本百分比。（有关标准误差的信息，请参见第11章。）

标准误差是置信区间的构建要素。置信区间是一个统计值加减一个误差幅度，而误差幅度就是你需要多少个标准误差才能得到你想要的置信水平。

每个置信水平都有一个相应的必须加或减的标准误差数量。这个标准误差数量被称为临界值。在使用Z分布查找标准误差数量的情况下（如本章后面所述），你将这个临界值称为Z*-值（发音为Z星值）。请参见表13-1，其中列出了一些常见置信水平的Z*-值。

随着置信水平的提高，标准误差的数量也会增加，因此误差边际会增加。

如果你想对结果有超过95%的信心，你需要加减大约两个标准误差之外的一些值。例如，要达到99%的置信水平，你需要加减大约两个半标准误差来获得你的误差边际（确切地说是2.58）。置信水平越高，z*-值越大，误差边际越大，置信区间就越宽（假设其他条件不变）。获得更高的置信水平需要付出一定的代价。

注意，我说的是“假设其他条件不变”。你可以通过增加样本量来抵消误差边际的增加。关于这一点，可以查看以下章节的更多内容。

误差边际与样本量之间的关系很简单：随着样本量的增加，误差边际减小，置信区间变得更窄。这个关系印证了你所期望的：你拥有的信息（数据）越多，你的结果就越准确。当然，这假定信息是好的、可信的信息（请参考第3章了解统计学可能出现的问题）。

本章置信区间的误差边际公式都包含样本量（n）在分母中。例如，样本均值的误差边际公式

（稍后会详细介绍），在分数的分母中有一个n（对于大多数误差边际公式来说都是这样）。随着n的增加，这个分数的分母增加，使得整体分数变小。这使得误差边际减小，从而产生一个更窄的置信区间。

当你需要高置信水平时，你必须增加z*-值和因此的误差边际，导致置信区间变得更宽，这并不好（参见前面的章节）。但你可以通过增加样本量来抵消这个更宽的置信区间，降低误差边际，从而缩小置信区间。

样本量的增加不仅可以确保你得到想要的置信水平，还可以确保你的置信区间宽度较小（这是你最终想要的）。你甚至可以在开始研究之前确定需要的样本量：如果你知道想要达到的误差边际，可以相应地设置样本量（有关更多信息，请参见后面的“确定所需样本量”一节）。

当你的统计量是一个百分比时（比如喜欢在夏天穿凉鞋的人的百分比），计算95%置信区间的一种简便方法是取1除以n的平方根（样本量）。你可以尝试不同的n值，看看误差边际如何受到影响。例如，从人口众多的群体中调查100人将产生大约

或±10%的误差边际（即置信区间的宽度为20%，相当大）。

然而，如果你调查1,000人，你的误差边际将显著减小，约为±3%；现在置信区间的宽度仅为6%。对2,500人的调查导致误差边际为±2%（因此宽度减小到4%）。考虑到人口的庞大（例如，美国人口超过3.1亿），能够通过如此小的样本量获得如此准确的结果令人惊讶。

然而，请记住，样本量不要增加得太大，因为有一个点会导致收益递减。例如，从样本量为2,500增加到5,000将将置信区间的宽度减小到大约2 * 1.4 = 2.8%，从4%下降。每次增加一个受访者，调查成本都会增加，因此为了将置信区间缩小不到1%，增加另外2,500人可能并不值得。

在任何数据分析问题的第一步（以及在批评他人的结果时），都要确保你拥有良好的数据。统计结果只有在数据质量高的情况下才能够准确，因此真正的准确性取决于数据的质量以及样本量。即使样本量很大，但如果存在很大的偏见（参见第16章），看起来可能有一个窄的置信区间，但这意味着什么都没有。这就像在射箭比赛中持续稳定地射箭，但最后发现一直在射向其他人的目标，你偏离的距离就是这么远。然而，在统计学领域，你不能准确地测量偏见；你只能通过设计良好的样本和研究来尽量减少它（请参见第16和17章）。

影响样本结果变异性的因素之一是人口本身包含变异性。例如，在像俄亥俄州哥伦布这样一个相当大的城市的住房人口中，不仅可以看到各种各样类型的住房，而且还有不同的大小和价格。而哥伦布市房屋价格的变异性应该比哥伦布市某个特定住宅开发区的房屋价格变异性更大。

这意味着，如果你从整个哥伦布市抽取一组住房样本并找出平均价格，误差边际应该比你从哥伦布市的那个单一住宅开发区抽取的样本更大，即使你有相同的置信水平和相同的样本量。

为什么呢？因为整个城市的房屋价格变异性更大，你的样本平均价格在样本之间会更多地发生变化，而如果你只从单一住宅开发区抽取样本，那里的价格往往很相似，因为在单一住宅开发区，房屋往往是可比较的。因此，如果你从整个哥伦布市抽样，为了获得与从那个单一住宅开发区抽取的样本相同的准确性，你需要抽更多的房屋。

人口的标准差用符号表示。请注意，在样本均值误差边际公式中，人口的标准差出现在分子中：