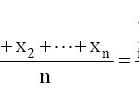,其中t*是t-分布中的临界值,具有n1 n2 – 2个自由度;n1和n2分别是两个样本的大小;s1和s2是两个样本的标准差。这个t*-值可以在t-表(见附录)中找到,通过交叉查看df = n1 n2 – 2的行和所需的置信水平的列,如表的最后一行所示。(见第10章。)在这里我们假设总体标准差是相似的;如果不是,可以通过使用标准误差和自由度进行修改。详见第15章比较两个均值一节的末尾。
在情况1中的玉米示例中,假设两个玉米品牌Corn-e-stats(组1)和Stats-o-sweet(组2)的平均玉米穗长度仍然相同:x̅1=8.5和x̅2=7.5英寸。但这次你不知道总体标准差,因此使用样本标准差 —— 假设它们分别是s1 = 0.40和s2 = 0.50英寸。在这种情况下,假设样本量n1和n2各为15。
计算置信区间时,首先需要在具有(15 15 – 2)= 28个自由度的t-分布中找到t*-值。 (假设置信水平仍为95%。)使用t-表(见附录),查看28个自由度的行和表示95%置信水平的列(参见表的最后一行上的标签);相交处的值为t*28 = 2.048。使用给定的其他信息,这两个品牌玉米平均玉米穗长度差异的95%置信区间是


这意味着在这种情况下,这两个品牌玉米平均玉米穗长度差异的95%置信区间是(0.0727, 1.9273)英寸,Corn-e-stats更胜一筹。(注意:如预期的那样,这个置信区间比请1中找到的要宽。)
估算两个比例的差异当两个被比较的群体的某一特征(例如对某个问题的支持/不支持)是分类的时候,人们希望报告这两个总体比例之间的差异 —— 例如,支持四天工作周的女性比例与支持四天工作周的男性比例之间的差异。要如何做到这一点呢?
你通过从每个群体中抽取样本,并使用两个样本比例之差,p1-p2 ,再加上或减去一个误差范围,来估算两个总体比例之差,p̂1 – p̂2。结果被称为两个总体比例差异的置信区间,p1 – p2。
计算两个总体比例差异的置信区间的公式是

,其中p̂1和n1分别是第一个样本的样本比例和样本大小,p̂2和n2分别是第二个样本的样本比例和样本大小。z*是适用于你所需置信水平的标准正态分布的值。(参考表13-1中的z*-值。)
要计算两个总体比例差异的置信区间,执行以下步骤:
- 确定置信水平并找到适当的z*-值。参考表13-1。
- 通过取第一个样本中在感兴趣的类别中的总数并除以样本大小n1,找到第一个样本的样本比例p̂1。同样,找到第二个样本的样本比例p̂2。
- 取两个样本比例之差,p̂1-p̂2 。
- 计算p̂1(1-p̂1)并除以n1。计算p̂2(1-p̂2)并除以n2。将这两个结果相加并取平方根。
- 用z*乘以步骤4的结果。这一步骤给出了误差范围。
- 从步骤5的误差范围中加减得到置信区间。置信区间的下限是减去误差范围,上限是加上误差范围。
- 这里给出的估算p1 – p2的置信区间的公式是在两个样本大小都足够大,满足中心极限定理可以使用z*-值的条件下使用的(参见第11章);这在例如使用大规模调查估算比例时成立。对于小样本量,置信区间超出了入门统计课程的范围。
假设你在拉斯维加斯商会工作,你希望以95%的置信度估算曾经去看过猫王模仿者的女性百分比与曾经去看过猫王模仿者的男性百分比之间的差异,以帮助确定如何营销你的娱乐活动。
- 因为你希望95%的置信区间,所以你的z*-值是1.96。
- 假设你随机抽取的100名女性中有53名看过猫王模仿者,所以p̂1=53/100=0.53 ,又因为37名男性中有37名曾经看过猫王模仿者,所以p̂2=37/110=0.34 。
- 这些样本比例之差(女性 - 男性)为0.53 – 0.34 = 0.19。
- 取 0.53 ∗ (1 – 0.53) 并除以100得到0.2491 ÷ 100 = 0.0025。然后取 0.34 ∗ (1 – 0.34) 并除以110得到0.2244 ÷ 110 = 0.0020。将这两个结果相加得到0.0025 0.0020 = 0.0045;平方根是0.0671。
- 1.96 ∗ 0.0671得到0.13,即13%,这是误差范围。
- 你的95%置信区间,女性看过猫王模仿者的百分比与男性看过的百分比之间的差异是0.19或19%(这是在步骤3中得到的),加减13%。区间的下限是0.19 – 0.13 = 0.06或6%;上限是0.19 0.13 = 0.32或32%。
- 在问题的背景下解释这些结果,你可以说,基于你的样本,以95%的置信度,女性看过猫王模仿者的百分比比男性高,这两个百分比之间的差异在6%到32%之间。
- 现在我在想,可能有些男人不会承认他们曾经看过猫王模仿者(尽管他们可能曾经在卡拉OK上假装是猫王)。这可能会对结果产生一些偏见。
- 注意,你可能会得到一个负值。例如,如果你交换了男性和女性,你会得到这个差异的-0.19。这没关系,但你可以通过让具有较大样本比例的组作为第一组(在这里是女性)来避免样本比例中的负差异。
当误差范围相对较小时,您可能希望说这些置信区间提供了参数的准确和可信赖的估计。然而,情况并非总是如此。
并非所有的估计都像来源可能希望你认为的那样准确和可靠。例如,基于2万次点击的网站调查结果可能根据公式具有较小的误差范围,但如果调查仅提供给偶然访问该网站的人,那么误差范围就毫无意义了。
换句话说,样本甚至不能被视为接近随机样本(从总体中选择的每个相同大小的样本都有被选择参与的相等机会)。尽管如此,这样的结果确实会被报告,连同其误差范围,使研究看起来很科学。小心这些虚假的结果!(有关误差范围限制的更多信息,请参见第12章。)
在基于某人的估计做出任何决定之前,请执行以下操作:
✓ 调查统计数据的创建方式;它应该是科学过程的结果,产生可靠、无偏、准确的数据。
✓ 寻找误差范围。如果没有报告,去查找原始来源。
✓ 记住,如果统计数据不可靠或包含偏差,误差范围将毫无意义。
(有关评估调查数据的信息,请参见第16章,有关实验中良好数据标准的信息,请参见第17章。)