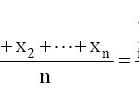区间估计的一般方法和步骤,区间估计的常用方法有矩估计法

；无论您得到什么数值，都要采用进一法处理样本大小。 （例如，如果您的计算结果是126.2人，您不能只有0.2个人 - 您需要整个人，因此通过进一法取为127人来包括。）

在此公式中，MOE是表示您想要的误差边际的数字，z*是与所需置信水平相对应的z*-值（来自表13-1；大多数人在95％的置信区间中使用1.96）。如果总体标准差未知，您可以对其进行最坏猜测，或者提前运行一项试验研究（小型试验研究），找到样本数据的标准差（s），并使用该数字。如果样本量非常小，这可能是有风险的，因为它不太可能反映整个人口；尽量获得尽可能大的试验研究，和对σ进行保守估计。

通常，小型试验研究是值得时间和精力的。您不仅将获得有助于确定良好样本大小的估计，还可能了解数据收集中可能出现的问题。

在本章中，我只包含了一个用于计算样本大小的公式：与总体均值的置信区间相关的公式。 （但是，您可以使用前一部分“考虑样本大小”中的快速简便公式来处理比例问题。）

以下是一个需要计算n以估计总体均值的示例。假设您想要估计大学生在便携式设备上存储的歌曲的平均数量。您希望误差边际不超过加减20首歌。您想要95％的置信区间。您应该对多少名学生进行抽样？

因为您想要95％的CI，z*是1.96（在表13-1中找到）；您知道您期望的MOE是20。现在，您需要一个总体标准偏差的数字，σ。由于不知道这个数字，因此您对35名学生进行试验研究，并发现样本的标准偏差（s）为148首歌 - 将此数字用作σ。使用样本大小公式

，您计算所需的样本大小是，进一法到211名学生（计算n时总是进一）。因此，您需要随机抽样至少211名大学生，以确保存储歌曲数量的误差不超过20。这就是为什么在这个公式中看到大于或等于符号的原因。

在计算样本大小时，无论结果的小数值是什么，您总是进一到最接近的整数（例如，0.37）。这是因为您希望误差边际不超过您声明的值。如果在小数值低于0.50时将其舍入（就像您在其他数学计算中通常做的那样），则您的MOE将比您想要的稍大。

当被测量的特征是分类的时候，例如对某个问题的意见（支持、反对或中立）、性别、政党或行为类型（驾驶时系不系安全带）等，大多数人都希望估计人口中属于感兴趣类别的人的比例（或百分比）。例如，考虑支持四天工作制的人的百分比、在上次选举中投票的共和党人的百分比或不系安全带的驾驶员的比例。在这些情况下，目标是使用样本比例，p̂，加上或减去一个误差边际，估计总体比例，p。其结果称为总体比例p的置信区间。

总体比例的置信区间公式为

，其中p̂是样本比例，n是样本大小，z*是所需置信水平的标准正态分布中的适当值。请参阅表13-1以获取某些置信水平的z*值。

计算总体比例的置信区间：

1. 确定置信水平，并找到适当的z*-值。请参阅表13-1以获取z*-值。
2. 通过将具有所关注特征的样本中的人数除以样本大小（n）来找到样本比例，p̂。注意：此结果应为介于0和1之间的小数值。
3. 将p̂乘以(1-p̂)然后除以n。
4. 对步骤3的结果取平方根。
5. 将您的答案乘以z*。此步骤给出误差边际。
6. 加上或减去误差边际以获得置信区间；置信区间的下限是减去误差边际，上限是加上误差边际。

在前面的例子中展示的总体比例p的置信区间公式是在样本大小足够大，使得中心极限定理可以发挥作用并允许我们使用z*-值的情况下使用的（请参阅第11章），这种情况通常出现在基于大规模调查估计比例的情况下（请参阅第9章）。对于小样本，比例的置信区间通常超出了入门统计课程的范围。

例如，假设你想要估计在某个十字路口等红灯的百分比。

1. 因为你想要一个95%的置信区间，所以你的z*-值是1.96。
2. 你随机抽取了100次经过这个路口的不同行程，并发现你53次遇到红灯，因此p̂=53/100=0.53。
3. 算出p̂(1-p̂)=0.53*(1-0.53)=0.2491/100=0.002491。
4. 取平方根得到0.0499。因此，误差边际为加减1.96 *（0.0499）= 0.0978，或9.78%。
5. 你在这个特定路口遇到红灯的百分比的95%置信区间是0.53（或53%），加减0.0978（进一为0.10或10%）。 （区间的下限为0.53 - 0.10 = 0.43或43％；区间的上限为0.53 0.10 = 0.63或63％。）
6. 为了在问题的背景下解释这些结果，你可以说，以95%的置信度，基于你的样本，你应该期望在这个路口遇到红灯的百分比在43%和63%之间。

在执行涉及样本百分比的任何计算时，请使用小数形式。计算完成后，通过乘以100转换为百分比。为避免舍入误差，始终保留至少2位小数。

许多调查和研究的目标是比较两个群体，例如男性与女性、低收入家庭与高收入家庭以及共和党人与民主党人。当进行比较的特征是数值型的（例如身高、体重或收入）时，感兴趣的对象是两个群体的均值（平均值）之间的差异。

例如，您可能想比较共和党人和民主党人的平均年龄差异，或者男性和女性的平均收入差异μ1-μ2。您通过从每个群体中抽取样本（比如，样本1和样本2），使用两个样本均值之差x̄1-x̄2，再加上或减去一个误差边际，来估计两个总体均值之间的差异。结果是两个总体均值差异的置信区间，μ1-μ2。置信区间的公式根据一定的条件而异，如下面的部分所示；我将其称为情况1和情况2。

情况1假设两个总体的标准差都已知。计算两个总体均值（平均值）之间的差异的置信区间的公式是

，其中x̄1和n1是第一个样本的均值和大小，和第一个总体的标准差σ1；x̄2和n2是第二个样本的均值和大小，和第二个总体的标准差σ2。这里z*是标准正态分布中与所需置信水平相对应的适当值。（参考表13-1，查看某些置信水平的z*值。）

要计算两个总体均值之间的差异的置信区间，请执行以下步骤：

1. 确定置信水平并找到适当的z*值。参考表13-1。
2. 确定x̅1、n1和σ1；找到x̅2、n2和σ2。
3. 计算样本均值之间的差异，(x̅1-x̅2)。
4. 将σ1其平方并除以n1；将σ2其平方并除以n2。将结果相加并取平方根。
5. 将步骤4的答案乘以z*。这个答案就是误差边际。
6. 将(x̅1-x̅2)加减误差边际以获得置信区间。置信区间的下限是x̅1-x̅2减去误差边际，而上限是x̅1-x̅2加上误差边际。

假设你想以95%的置信度估算两个甜玉米品种（它们在相同条件下生长相同的天数）的玉米穗的平均长度之间的差异。将这两个品种分别称为Corn-e-stats和Stats-o-sweet。假设根据先前的研究，Corn-e-stats和Stats-o-sweet的总体标准差分别为0.35英寸和0.45英寸。

1. 因为你想要95%的置信区间，所以z*是1.96。
2. 假设你对Corn-e-stats品种的100个玉米穗进行了随机抽样，平均长度为8.5英寸，而对Stats-o-sweet品种的110个玉米穗进行了随机抽样，平均长度为7.5英寸。因此，你掌握的信息是：x̅1=8.5，σ1=0.35，n1 = 100，x̅2=7.5，σ2=0.45，n2 = 110。
3. 从第3步得到的样本均值之差，x̅1-x̅2，为8.5 - 7.5 = 1英寸。这意味着Corn-e-stats的平均值减去Stats-o-sweet的平均值为正，从这个样本来看，Corn-e-stats是这两个品种中较大的一个。然而，这种差异是否足以推广到整个总体呢？这就是这个置信区间将帮助你决定的地方。
4. 将σ1（0.35）平方得到0.1225；除以100得到0.0012。将σ2（0.45）平方并除以110得到0.2025 ÷ 110 = 0.0018。两者之和是0.0012 0.0018 = 0.0030；平方根是0.0547英寸（如果没有进行进一）。
5. 将1.96乘以0.0547得到0.1072英寸，这就是误差边际。
6. 你两个甜玉米品种的平均长度差异的95%置信区间为1英寸，加减0.1072英寸。（区间的下限是1 - 0.1072 = 0.8928英寸；上限是1 0.1072 = 1.1072英寸。）请注意，此区间中的所有值都是正值。这意味着基于你的数据，Corn-e-stats的长度估计比Stats-o-sweet更长。

1. 要在问题的背景下解释这些结果，你可以说，以95%的置信度，基于你的样本，Corn-e-stats品种的平均长度比Stats-o-sweet品种长，估计差异在0.8928到1.1072英寸之间。

1. 请注意，差异x̅1-x̅2可能会得到负值。例如，如果你交换了两个品种的位置，你将得到差异为-1。你会说，在样本中，Stats-o-sweet的平均长度比Corn-e-stats短了一英寸（这是用不同的说法表达的相同结论）。

1. 如果你希望避免样本均值差异的负值，始终将具有较大样本均值的组作为第一组，这样你所有的差异将是正值（这是我的做法）。

在许多情况下，你不知道总体标准差，而是用样本标准差s1和s2来估算或样本量较小（小于30），你无法确定你的数据是否来自正态分布。

情况2下两个总体均值差异的置信区间为