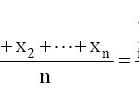,现在由于方差未知,则这区间的端点算不出来。一种解救办法是用样本的标准差s,经修正为无偏估计的s1作为σ的估计以代替

得出的区间估计为

由于我们对上面区间估计的计算是根据

服从标准正态分布N(0,1)这个性质的,用s1代替后,由于s1本身就是从样本算出的,它有随机性而非常数,故代替后的变量已不再是服从标准正态分布。它的分布是英国统计学家哥色特在1908年发现的,称为自由度为n-1的t分布,常记为tn-1。此分布的形状与标准正态分布很相似,在外表上无法区别,理论上可以证明,当样本大小n愈来愈大,t分布愈来愈接近于标准正态分布。大样本的情况将在接下来介绍,但针对总体服从正态分布,方差未知,又是小样本的情况,t分布将给我们的区间估计带来帮助。
由于分布tn-1已不是标准正态分布,与置信系数0.95,0.99和0.90等对应的,已不是前面指出的1.96,2.576和1.645,而是比较复杂,因为它与自由度n-1有关。我们约定用tn-1(置信系数)记相对应的系数,修正后的区间估计是