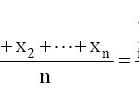区间估计
前文我们说到,标准差可以在平均意义上反映样本均值的精度,但是从区间估计的角度看,仅凭标准差已不能给出什么带普遍性的结论,而必须结合指标的分布去考察才行。
由于在实际问题中分布是各式各样的,这就注定了不可能提出一种简易可行、处处适用的方法。幸好,上文提到的正态分布有很大的普遍性,因此,针对这种分布提出的解法(即得到给定置信系数的区间估计,置信系数:把未知的均值估计在某一区间内,其正确的机会),有相当程度的普遍意义。另外,对一般的(可以是非正态的)分布而言,只要样本大小足够大,基于正态分布的解法仍能适用,只是从理论上说,这种解法是近似地而非确切的。下面分三种情况介绍相应的解法:
1) 总体中个体指标X的分布是正态的,即X~N(a,σ^2),其中方差已知,要估计的是均值.
从总体中抽取了n个样本X1,…,Xn,则样本均值

,于是标准化变量

服从标准正态分布N(0,1)
我们知道标准正态密度曲线在-1到1之间的那部分面积是0.683(即总体中指标值介于±1之间的那些个体,在总体中所占比率为0.683)。根据这个结论,不等式

实现的机会为0.683。以上不等式可改写为