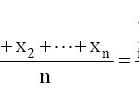区间估计的基本思想和步骤,点估计和区间估计的定义与优缺点

未知的a落在该区间内的置信系数为0.683。

同理，我们可以得到一系列的区间估计：

以上，可以看出，置信系数取得越高（即对估计越有把握），相对应付出的代价就是估计区间变大了。

一旦取定了一个置信系数，则区间长度也定下来了。

例如，取置信系数为0.95，则区间长度为

如果l太大，则估计很粗糙并且实际意义也很小。我们不能靠牺牲置信系数来降低这个长度，因为这会使估计变得很不可靠，用起来有危险。解决办法是选择适当的样本大小n。由上面求l的式子可知，如果我们指定区间之长不能超过某个限度l₀，则n必须满足：

2） 总体中个体指标X的分布是正态的，即X~N(a,σ^2)，其中方差未知，要估计的是均值.

例如，取置信系数为0.95，在方差已知的情况下，则用区间估计