对于更多的自变量,视觉理解更抽象。对于p个独立变量,数据点(x1,x2,x3 ......,xp,y)存在于p 1维空间中。真正重要的是线性模型(p维)可以用p 1系数β0,β1,...,βp表示,因此y近似为方程y =β0 β1* x1 β2* x2 ... βp* xp。
你需要知道这些
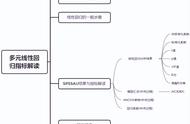
多元线性回归有两种类型:普通最小二乘法(OLS)(https://www.albert.io/blog/key-assumptions-of-ols-econometrics-review/)和广义最小二乘法(GLS)(https://www.statlect.com/fundamentals-of-statistics/generalized-least-squares)。两者之间的主要区别在于,OLS假设任意两个自变量之间没有很强的相关性,GLS通过转换数据,然后使用OLS来构建具有转换数据的模型来处理相关的自变量。
这些过程使用OLS的方法。因此,要构建成功的模型,首先应该考虑变量之间的关系。将卧室和住宿作为两个独立的自变量包含在一起可能不是一个好主意,因为卧室数量和容纳的客人数量可能具有很强的正相关性。另一方面,评论数量和房间数量之间没有明确的逻辑关系。对于定量的分析,需要选择自变量,使每对都具有接近零的Pearson相关系数(见下文)。(https://www.spss-tutorials.com/pearson-correlation-coefficient/)
多个LR在行动
好吧,让我们看看一组在Neo4j中构建的多元线性回归模型的查询。
建立
下载并安装最新的线性回归版本中的jar文件。(https://github.com/neo4j-graph-analytics/ml-models/releases/latest)运行:从Neo4j浏览器中播放http://guides.neo4j.com/listings并按照导入查询创建Will的短期租赁列表图表。有关安装线性回归程序和导入Austin租赁数据集的更全面指南,请参阅我之前的帖子。
拆分训练和测试数据
导入数据集并安装后,我们将数据集拆分为75:25(training:testing)样本。让我们从上次的最终模型开始构建,并且只考虑至少有一次客户评论的列表。标签75%:Train。

添加:Test标签到剩余的25%。

量化相关性
如果你想知道自变量之间的Pearson相关性,请使用函数regression.linear.correlation(List <Double> first,List <Double> second)。该函数的List <Double>输入之一包含来自许多列表的聚合"评论数"数据,并且通过聚合来自每个列表的关系来计算每个"评论数"。我们不能在同一次查询中执行两个级别的聚合(collect(count(r)))。 因此,我们必须执行两次查询。
首先在数据集列表中存储num_reviews。

然后从所有列表中收集(num_reviews,rooms)数据并计算相关性。