回归分析实质上就是研究一个或多个自变量X对一个因变量Y(定量数据)的影响关系情况。
当自变量为1个时,是一元线性回归,又称作简单线性回归;自变量为2个及以上时,称为多元线性回归。例如:研究吸烟、喝酒、久坐对高血压患病的影响关系等。
SPSSAU操作SPSSAU左侧仪表盘“通用方法”→“线性回归”;

回归分析用于研究X(定量或定类)对Y(定量)的影响关系,是否有影响关系,影响方向及影响程度情况如何。
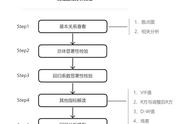
第一:首先分析模型拟合情况,即通过R方值分析模型拟合情况,以及可对VIF值进行分析,判断模型是否存在共线性问题【共线性问题可使用岭回归或者逐步回归进行解决】;
第二:写出模型公式(可选);
第三:分析X的显著性;如果呈现出显著性(p值小于0.05或0.01);则说明X对Y有影响关系,接着具体分析影响关系方向;
第四:结合回归系数B值,对比分析X对Y的影响程度(可选);
第五:对分析进行总结。
回归分析之前,可使用箱盒图查看是否有异常数据,或使用散点图直观展示X和Y之间的关联关系;回归分析之后,可使用正态图观察和展示保存的残差值正态性情况;或使用散点图观察和展示回归模型异方差情况【残差与X间的散点完全没有关系则无异方差】。
SPSSAU结果与指标解读1.线性回归分析结果