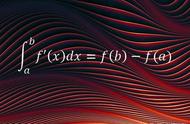伯克利的,比rudin要容易读些

包含欧氏空间上的勒贝格积分,这个废话比较多,所以更容易看

齐民友先生,一贯的循循善诱
三 、微积分本身的进阶第一个方向是几何,就是外微分和微分流形等;
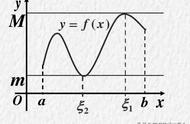
第二个方向是实变函数论,或者实分析、测度论;怎么说呢,实用的积分有很多种,不同的积分定义和适用范围当然不一样:最关键的莫过于积分的存在性或者收敛性。明白的说,虽然很难,但是如果你在同济高数后面再也没见过这些,这也太遗憾了:你在求导之前还问问可导不可导,同样还有可积不可积;这种导数不行,大不了换另外的导数;这种积分不行,大不了换一种积分。如果你还能证明几个定理,或者发明一个计算步骤,那就是数学家了,至少也是有兴趣了。
我很痛心,同济高数给你的伤害:上来就链式法则、换元法、求原函数,微分方程上来就分离变量。。。。虽然这些有根本的重要性。但是人类最大的优势是思考,而不是计算——计算器、计算机不要面子啊?
第三个就是微积分和线性代数一起的进阶,泛函分析。推广到无穷维。打算以后再推荐书。
四、总结真正意义上的学习,建立在明确的学习目标之上。不应该建立在考试的压力上。
真正意义上的学习,需要好书、好视频;真的不一定要上课,实在不去不行,可以不带脑子和情绪。
真正意义上的学习,不能只看一本书。不能只用一种方式看书,可以反复背,也可以抄;可以浏览,也可以精读;更可以坚决扔进垃圾桶。
真正意义上的学习,可能应该考试完了才开始,或许不该停下来。自己的学习,学什么,怎么学,学到什么程度,自己说了算。
罗里吧嗦一大堆,感谢阅读。
我是菜鸡速通两个基础,欢迎关注,更欢迎批评。