基本函数的单调性定义,基本函数的单调性怎么判断

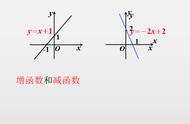
下面我们来看下面几个例题：

2．判断抽象函数单调性的方法

如果一个函数没有给出具体解析式，那么这样的的函数叫做抽象函数。抽象函数没有具体的解析式，需充分提取题目条件给出的信息。

2.1 定义法

通过作差(或者作商)，根据题目提出的信息进行变形，然后与0（或者1）比较大小关系来判断其函数单调性。通常有以下几种方法：

2.1.1 凑差法

根据单调函数的定义，设法从题目中“凑出”“f(x₁)-f(x₂)”的形式，然后比较f(x₁)-f(x₂)与0的大小关系。

例11.已知函数f(x)对任意实数m、n均有f(m n)=f(m) f(n)，且当m>0时，

f(m)>0，试讨论函数f(x)的单调性。

解：由题得f(m n)-f(m)=f(n)，

令x₁=m n,x₂=m，且x₁>x₂，则n=x₁-x₂>0

又由题意当m>0时，f(m)>0,得

f(x₁)-f(x₂)=f(m n)-f(m)=f(n)>0，

所以函数f(x)为增函数。

2.1.2添项法

弄清题目中的结构特点，采用加减添项或乘除添项，以达到能判断“f(x₁)-f(x₂)”与0大小关系的目的。

例12.（同例11）已知函数f(x)对任意实数m、n均有f(m n)=f(m) f(n)，且当m>0时，f(m)>0，试讨论函数f(x)的单调性。

解:任取x_1、x₂ ∈R，x₁<x₂ ，则x₂-x₁＞0,

f(x₂)-f(x₁)=f[(x₂-x₁) x₁]-f(x₁)

由题意函数f(x)对任意实数m、n均有f(m n)=f(m) f(n)

且当m>0时，f(m)>0,得

f(x₂)-f(x₁)=f(x₂-x₁)>0，

所以函数f(x)为增函数。

2.1.3 增量法

由单调性的定义出发，任取x_1、x₂ ∈R，x₁<x₂ 设x₂=x₁ γ（γ>0）,然后联系题目提取的信息给出解答。

例13.已知函数f(x)对任意实数m、n均有f(m n)=f(m) f(n)，且当m>0时，f(m)>0，试讨论函数f(x)的单调性。

解：任取x_1、x₂ ∈R，x₁<x₂ 设x₂=x₁ γ（γ>0）

由题意函数f(x)对任意实数m、n均有f(m n)=f(m) f(n)，得

f(x₂)-f(x₁)=f(x₁ γ)-f(x₁)=f(γ)

又由当m>0时，f(m)>0得

f(x₂)-f(x₁)=f(γ)>0

所以函数f(x)为增函数。

2.1.4 放缩法

利用放缩法，判断f(x₁)与f(x₂)的大小关系，从而得f(x)在其定义域内的单调性。

对于抽象函数，由于抽象函数没有具体的解析式，因此需充分提取题目条件给出的信息,观察结构特点。用定义法判定抽象函数单调性比较适用于那种对于定义域内任意两个数x_1、x₂ ，当x₁<x₂ 时，容易得出f(x₁)-f(x₂)与0大小关系的函数。定义法是最直接的方法，思路也比较清晰，在解题中灵活选择凑差法、添项法、增量法、放缩法等恰当的方法，可使解题过程更加简单方便。

总结：函数单调性是函数的一个非常重要的性质，本文从单调性的定义入手，总结了判断单调性的常见方法。本文把函数分为具体函数和抽象函数两大类进行讨论，对于每类函数都给出了判定单调性的若干方法。对于具体的函数，我们可以用多种方法去判断其单调性，特别地导数法是普遍适用的，若借助于计算机，那么图像法也是最简单最直观的。对于抽象函数的单调性问题，我们给出了用定义法及列表法。这种题型不仅抽象，而且综合性较强，对学生的思维能力有很高的要求，学生往往很难发现数学符号与数学语言之间的内在关系。因此在判断函数单调性的问题上，应灵活选择恰当的方法，从而使解题过程最简单。

注意：文中讲的是函数单调性的判断方法，要注意区分函数单调性的证明与判断的不同。函数单调性的证明只能用定义法和导数法，而函数单调性的判断除定义法和导数法，还可以使用文中介绍的各种方法进行判断。