基本函数的单调性定义,基本函数的单调性怎么判断

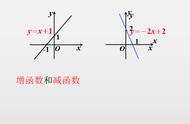
对于一些常用的关于函数单调的性质可总结如下一些结论：

⑴．f(x)与f(x) C单调性相同。（C为常数）

⑵．当k>0时，f(x)与kf(x)具有相同的单调性；当k<0时， f(x)与kf(x)具有相反的单调性。

⑶．当f(x)恒不等于零时，f(x)与1/f(x)具有相反的单调性。

⑷．当f(x)、g(x)在D上都是增（减）函数时，则f(x)＋g(x)在D上是增（减）函数。

⑸．当f(x)、g(x)在D上都是增（减）函数且两者都恒大于0时，f(x)g(x)在D上是增（减）函数；当f(x)、g(x)在D上都是增（减）函数且两者都恒小于0时，f(x)g(x)在D上是减（增）函数。

⑹．设y=f(x),x∈D为严格增（减）函数，则f(x)必有反函数，且反函数在其定义域f(D)上也是严格增（减）函数。

我们可以借助以上简单函数的单调性来判断函数的单调性，下面我们来看以下几个例子：

函数性质法只能借助于我们熟悉的单调函数去判断一些函数的单调性，因此首先把函数等价地转化成我们熟悉的单调函数的四则混合运算的形式，然后利用函数单调性的性质去判断，但有些函数不能化成简单单调函数四则混合运算形式就不能采用这种方法。

1.3 图像法

用函数图像来判断函数单调性的方法叫图像法。根据单调函数的图像特征，若函数f(x)的图像在区间D上从左往右逐渐上升则函数f(x)在区间D上是增函数；若函数f(x)图像在区间D上从左往右逐渐下降则函数f(x)在区间D上是减函数。

例5. 如图是定义在闭区间[-5,5]上的函数的图像，试判断其单调性。

解：由图像可知：函数y=f(x)的单调区间有[-5,-2），[-2,1），[1,3），[3,5）。

其中函数y=f(x)在区间[-5,-2），[1,3）上的图像是从左往右逐渐下降的，则函数y=f(x)在区间[-5,-2），[1,3）为减函数；函数y=f(x)在区间[-2,1），[3,5]上的图像是从往右逐渐上升的，则函数y=f(x)在区间[-2,1），[3,5]上是增函数。

例6.利用函数图像判断函数f(x)=x 1；‚g(x)=2^x；ƒh(x)=2^x x 1在[-3,3]上的单调性。

分析：观察三个函数，易见h(x)=f(x) g(x)，作图一般步骤为列表、描点、作图。首先作出f(x)=x 1和g(x)=2^x的图像，再利用物理学上波的叠加就可以大致作出h(x)=2^x x 1的图像，最后利用图像判断函数h(x)=2^x x 1的单调性。

解:作图像如下所示：