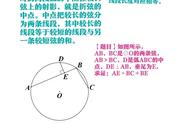
如图,在CD上截取DG=DB
∵MD⊥BG
∴MB=MG,∠MGB=∠MBC=∠MAC
∵M是弧ABC的中点
∴∠MAC=∠MCA=∠MGB
即∠MGB=∠MCB ∠BCA=∠MCB ∠BMA
又∠MGB=∠MCB ∠GMC
∴∠BMA=∠GMC
∵MA=MC
∴△MBA≌△MGC(SAS)
∴AB=GC
∴CD=CG GD=AB BD
方法4:截长法2

如图,在CD上截取CG=AB
∵M是弧ABC的中点
∴MA=MC
∵∠BAM=∠BCM
∴△MBA≌△MGC(SAS)
∴MB=MG
∵MD⊥BG
∴BD=DG
∴CD=CG GD=AB BD
方法5:垂线法
如图,作MH⊥射线AB,垂足为H。
∵M是弧ABC的中点
∴MA=MC
∵MD⊥BC
∴∠MDC=90°=∠H
∵∠MAB=∠MCB
∴△MHA≌△MDC(AAS)
∴AH=CD,MH=MD
又∵MB=MB
∴Rt△MHB≌Rt△MDB(HL)
∴HB=BD
∴CD=AH=AB BH=AB BD
方法6:圆周角法

延长MD交圆O于E,连接EC,EA,
延长EA交CB延长线于F.
∵M为AMC中点
∴∠1=∠2
∵ MD⊥BC
∴∠EDF=∠EDC=90°,
∵ED=ED
∴△EDF≅△EDC
∴∠C=∠F,DF=DC
∵A.B,C,E 四点共圆
∴∠C ∠BAE=180°.
而∠3 ∠BAE=180°
∴∠C=∠3
∴∠F=∠3
∴BF=AB
∴CD=FD=BF BD=AB BD
典例1 ☆☆☆☆☆
如图,已知点A,B,C,D顺次在圆O上,AB=BD,BM⊥AC,垂为 M.
证明∶AM=DC+CM.