平面几何中的“角格点”问题,既有难度、又有趣味;既有规律、又有技巧。有时我们抓住其的某一个特性作为切入点,就能找到多条思路。今举经典难题一例,利用对称显示原三角形外心为突破口,说说其的三个思路,供参考:
【例题】(如图)△ABC中,点D为其内一点,且有:∠ABD=30º,∠DBC=42º,∠ACD=18º,∠DCB=54º,求:∠BAD的度数

【思路一】(作对称显外心、造外心寻外心)
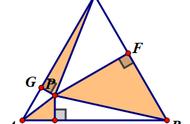
(1)已知可得:AB=AC,∠BAC=36º,作BC边上的中垂线AE,垂足为E,即等腰△ABC的对称轴,∴∠BAE=∠CAE=18º
(2)延长CD交AE于点O,连OB,则∠OCA=∠OAC=18º,∴OA=OC,由对称性知,OA=OC=OB,点O为△ABC外心,∠BOC=72º
(3)以OA为边作正三角形△AOF,连BF,则∠ABF=30º,∴∠OBF=12º=∠OFB,得点D在BF边上,在△FOD中易知:∠FDO=84º=∠FOD,∴FD=FO=FA,所以:点F为△AOD的外心,所以:∠OAD=12º/2=6º
(4)所以:∠BAD=18º+6º=24º
【思路二】(对称性、造外心、找外心)

(1)知得:∠BAC=36º,AB=AC,作底边BC上中垂线交BD于点E,∴∠EAB=∠EAC=18º,延长CD交AE于点O连OB,易得:OA=OC=OB,∠BOC=72º,∠ABO=18º,∠OBD=12º
(2)以OA为边如图作正△OAF,连FC交OB于点G,连AG,由OA=OC=OF,∴点O为△AFC外心,∴∠ACF=60º/2=30º,∠OFC=∠OCF=12º,∠GCB=42º,点E落在FC上
(3)由对称性得:BG=CD,∴△ABG≌△ACD
(4)△FGO中∠FGO=72º+12º=84º=∠FOG,∴FG=FO=FA,点F为△AOG的外心,∠GAO=6º
(5)所以:∠BAG=18º-6º=12º=∠CAD,∴∠BAD=36º-12º=24º
【思路三】(作外心利用30º角找外心)

(1)作△ABC的外接圆⊙O,连接半径得OA=OB=OC,知:∠BAC=36º,∴∠BOC=72º,∴∠OBC=∠OCB=54º,∴点D在半径OC上,由:AB=AC,∴∠BAO=∠CAO=18º
(2)延长BD交⊙O于点E,连OE、AE,由己知∠ABE=30º,∴∠AOE=60º,△OAE为正三角形,∴EA=EO,易得:∠OBE=12º=∠OEB,∴∠ODE=72º+12º=84º,而∠DOE=180º-84º-12º=84º,∴∠ODE=∠DOE,∴EO=ED
(3)所以:EO=ED=EA,点E为△AOD的外心,∴∠OAD=∠OED/2=6º,∴∠BAD=24º
以上一题三思路,“道听度说”供参考。