图3 静电场、磁场与引力场
在会计算点电荷电场的基础上,人们还想知道一般带电体产生的电场强度E 和电势φ 的定量计算的数学方法。笛卡尔在关于自然科学的哲学本质上提出了一个“指导法则”:为了解决所遇到的难题必须把它们分成几部分,必须从最简单的(对象)开始,逐步进入到对复杂的(对象)认识。这种方法系统地渗透在从力学、电学到原子物理等物理学各个分支中。例如,运动的合成、力的合成等都体现了这样的思想,其前提条件是“部分”之间的相加必须服从“叠加原理”。力学部分从质点运动开始,再到质点系;电学部分从点电荷产生的电场引入,再到电荷系;对于连续体层次上的力学和电学的讨论方法体现了“从简单到复杂”的思维原则。当然,线性系统只是自然界的一种近似的、理想化的模型系统,真实的系统更多的是非线性系统。
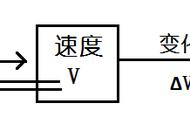
在力学中,描述质点运动状态的物理量是位置x、动量p 等物理量,这些物理量是质点所在空间位置的函数。位置的改变产生位移Δx,位置随时间的改变得出速度v,速度随时间的改变产生加速度a。在力学中描述质点状态的物理量是位置x 和速度v,它们之间体现的是在时间上的变化率关系

。在静电学中描述电场状态的物理量是电场强度E 和电势φ,它们的定义之间体现的是在空间上的变化率关系

,从时间变化率的关系到空间变化率的关系。
力学平衡是指质点受两个外力作用达到平衡,合力为零,质点保持静止或匀速直线运动状态;如果把“静止”称为“静平衡”,那么“匀速直线运动”就可以称为“动平衡”。热学中的平衡态是指系统内部没有“质量流”和“热量流”,不随时间改变的宏观状态,但系统内部分子还在做无规则的热运动,因此称为“热动平衡状态”。与此类似,电学中的静电平衡态指的是受外部电场和内部电场的共同作用,导体内部处处净电荷为零以及内部电场强度为零,导体表面没有电荷定向移动的状态,也是另一个意义上的“动态平衡”,是电场强度和电荷分布之间相互影响而达到的一种动态平衡。因此,导体的静电平衡在平衡思想上是对力学平衡和热学平衡的横向联系的深化和发展。
在物理系统里,一个粒子从起点移动到终点,若受作用力且该作用力所做的功不因为路径的不同而改变,则称此力为保守力。如果物体沿闭合路径绕行一周,则保守力对物体所做的功恒为零,即势能与其他形式的能量转化为零,于是系统间的势能不变。当相对位置确定时,它们之间的势能就是确定的、唯一的,因此保守力是与势能关系密切的概念。重力、万有引力、弹力、静电力和分子力等都具有这个性质,重力对应着重力势能,弹力对应弹性势能,静电力对应着电势能,分子力对应着分子势能等。因此,卫星绕着地球转,地球绕着太阳转,电子绕着原子核转等宏观和微观的稳定模型系统,都属于保守力系统。
04
结语:横向联系拓展物理视界
横向联系不仅适用于物理学科内不同内容的联系,也适用于不同学科间的关联拓展。例如变化量与变化率、稳定性与变化、结构与功能、系统和系统模型等跨学科的概念在其他学科中也有着广泛的应用。进行学科内以及跨学科间概念的横向联系,不仅能深化对概念和规律的认识,而且能拓展我们的物理视界,更是解决问题和认识未知的重要方式。
参考文献
[1] 皮埃尔·迪昂. 物理学理论的目的与结构. 北京:商务印书馆,2011
[2] 朱鋐雄. 物理学思想概论. 北京:清华大学出版社,2009
[3] 郭奕玲,沈慧君. 物理学史. 北京:清华大学出版社,2005
原标题:万象同一理,触类可旁通
来源:中国物理学会期刊网
编辑:谦、yrLewis