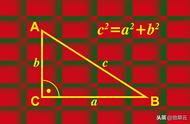
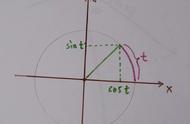
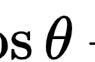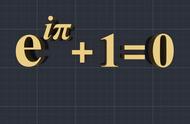也可以表示为£[f(t)],其中L实际应为L的花体式样,也就是拉普拉斯第一个字母,可是我打不出来真正的花体······

拉普拉斯变换的条件,必须是的F(S)等号右边的广义积分在S区域内收敛,所谓收敛其实就是指该函数的变量t在趋向无穷的时候,其通项的值趋向于某一个数值。如下图所示,当t趋向无穷时,通项值趋向于0。这也是拉普拉斯变换存在的先决条件,e^(-σt)也称为收敛因子(σ为任意实数)。

也就是说,不管函数f(t)是否收敛,但是增加了收敛因子后,它一定是收敛的,那么它的拉普拉斯变换就一定存在了(这货是不是辣条啊,没有它搞不定的@@)。

举一个例子吧,假设一个一次函数f(t)=mt(t≥0,m为常数),求它的拉普拉斯变换,求解过程如下: