我:聪明……
小明:大师,我买个彩票,还要发挥“愚公移山”的精神啊!!!

我:开个玩笑嘛……
小明:我理解你的意思了,“买彩票中大奖“的概率非常低,但是,试验次数无限增大(不断的买)的话,这个事件(买彩票中大奖)必然会发生。
我:回到你的问题。对于休哈特流派的常规控制图,控制界限的制定准则是这样的:
过程稳定的情况下,一个点在控制界限内(不出界)的概率是99.73%,出界概率是0.27%。
小明:这个我知道啊!!!赶紧说重点……
我:在过程稳定的情况下,2个点都在控制界限内(不出界)的概率应该是多少呢?
小明:应该是0.9973×0.9973吧,也就是0.9973的2次方……
我:假设有n个点,这些点都在控制界限内(不出界)的概率应该是多少呢?
小明:应该是0.9973的n次方……
我:供应商提供的XX产品的控制图,大概有多少点呢?
小明:大约有2500个点。
我:在过程稳定的情况下,2500个点都在控制界限内(不出界)的概率应该是多少呢?
小明:我用计算器算一下。0.9973^2500=0.00116=0.116%……这个概率太低了吧,比0.27%还要低呢!!!

我:换句话说,如果数据都是真实的,对于常规控制图,在过程稳定情况下,2500个点都在控制界限内(不出界)的概率非常低,才千分之一左右(几乎接近“0”)。
小明:那么,供应商伪造数据的可能性非常高,呵呵……
我:所以,“点超出控制界限就判异”,这句话是有问题的。
小明:是否可以这么理解,(长时间)一直没有“出界点”,反而是异常的情况,应该判异。
我:是的。接下来,再给你讲点干货……
对于常规控制图,【从一个很长的时间段内来看】,如果超出控制界限的点的比率不超过2%,那么就不能认为过程发生了异常……
小明:为什么是2%的比率呢?
我:可以计算,在过程稳定情况下,100个点中,有n个点(0个点、1个点、2个点、3个点……)超出控制界限的概率。
小明:计算概率的公式告诉我一下吧?
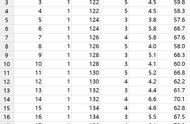
我:下次培训时给你详细解释公式,可以借用Minitab的概率分布图功能。我上次给过你一个图片,是常规控制图的概率计算分布图。在电脑里面好好找找……

小明:找到了。从图片信息来看,在过程稳定的情况下,对于100个点而言,“有0个点出界“&”有1个点出界“&”有2个点出界”的概率之和是99.74%(0.9974)。非常接近于“一个点在控制界限内(不出界)的概率——99.73%(0.9973)”。
我:因此,在100个点中,有“2个点以上”超出控制界限,才能认为过程异常。也就是2%比率的由来……
小明:突然想起一件事情,你们公司SPC系统的“判异原因”分析代码,有一个是“其它”……我一直很疑惑。现在看起来,是为了这种情况而准备的吧……
我:聪明……但是,如果你在SPC系统里面设置了【判异原因—“其它”】,作业员偷懒,每次判异都选择“其它”,怎么办?
小明:我记得,每次分析过程的时候,你都会先筛选出【判异原因—“其它”】的点的数量。这么做的目的是:为了和2%的比率进行比对,是吧……
我:嗯嗯,接下来,我想说的是……