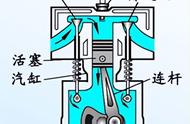
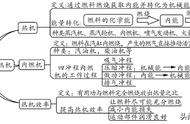
怀着激动的心情,在正式开始研究熵之前,我们还需要了解一下工作于两个热源之间的循环过程。为引入熵的概念做一下知识上的铺垫。如果一个循环过程是准静态的,则它的每一步都是热力学平衡态,在两个独立状态变量构成的平面图上,可以用一条闭合曲线来表示它。但如果是非静态的过程,照例是画不出曲线的。这里约定不管是否是准静态过程,我们都可以用一闭合曲线来表示循环过程。
一个热机工作于两个热源T1和T2之间(T1>T2),在一个循环过程中,从T1吸热Q1,对外做功W,向T2放热Q2,则热机的效率为η=W/Q1

卡诺定理为:所有工作于同温度热源和同温度冷源之间的循环过程以可逆循环的效率最大。这个定理可以从热力学第二定律证明。
一个可逆循环和一个不可逆循环工作于同一个热源(T1)和同一个冷源(T2)之间,可逆循环(R)从热源吸热Q1,对外做功W,向冷源放热Q2,它的效率为ηR=W/Q1
不可逆循环(I)从热源吸热Q1,对外做功W',向冷源放热Q2,它的效率为ηI=W'/Q1

咱们用反证法来证明一下卡诺定理。
如果卡诺定理是错误的,即ηI>ηR,那么W’>W,这样我们就可以把两个循环联合起来工作,让可逆循环(R)倒过来工作,由于不可逆循环(I)做的功大,故分出一部分W作为对可逆循环做的功,另一部分W’-W为不可逆循环对外界做的功,联合循环的结果是:不可逆循环从热源吸热Q1,可逆循环又想冷源放热Q1,高温热源无变化,联合循环做功W'-W,而从冷源吸热为Q2-Q2' ,由于W'=Q1-Q2’,W=Q1-Q2
可以得到W'-W=Q2-Q2’,最终结果是从单一热源吸收的热量全部转变成功,而未发生其它变化。这就违背了热力学第二定律的开尔文解释,所以假设的前提是错误的,只能是ηI≤ηR,这就证明了卡诺定理。

咱们接下来证明卡诺定理的一个推论:工作与同温热源和同温冷源之间的可逆循环的效率都相同。
假设有两个可逆循环R1和R2 ,由于R1是可逆循环,所以有ηR1≥ηR2
又因为R2 也是可逆循环,则ηR2≥ηR1
如果我们要求上门两个式子都成立只能是ηR1=ηR2,这里面的证明都不涉及到具体的工作物质,所以这个推论也与工作物质没有关系。我们在以后的文章中来说明,如何从卡诺定理的这个推论中得出热力学温标和态函数熵。
在距离熵越来越近的过程中,老郭激动的心情渐渐平复了,希望我能继续保持理性,跟各位小伙伴继续探讨一下熵的本质。然后嘛,咱们再利用熵去寻找一个大秘密……。哈哈,胃口是不是吊得有点太高了啊,也许老郭啥也发现不了,其实这也是很可能的,毕竟,老郭能力不高,水平也有限。没准就是在那自己意淫,不多说了。提前预报,下一篇《热力学温标》。
,