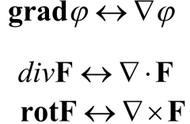多于二元的函数
更多元的函数偏导数类似二元函数定义, 只是对某一个变量求导, 而其余自变量为常数.
偏导数和连续性一元函数导数即意味着连续, 但二元函数 f(x,y) 不同, 在一个点不连续, 但对 x 和 y 可以求偏导.

二阶导数就是对函数求导两次, 但注意求导次序如果是先对y 求偏导, 再对 x 求偏导应该这样的写法:

在计算二阶混合导数时候, 可以按任意次序微分.
可微性 Differentiability如果 fx(x0,y0 和 fy(x0,y0) 存在, 并且 Δz 满足下面的等式:

其中当 (Δx,Δy)→(0,0) 时 (ϵ1,ϵ2)→(0,0), 则函数 z=f(x,y) 是在 (x0,y0) 点可微的.
如果它在定义域内的每个点都是可微的, 则说 f 是可微的.
多元函数偏导存在且连续推出函数可微, 但反之不成立, 这点与一元函数不同.(完)
,「予人玫瑰, 手留余香」
转发既是支持, 我们会努力走得更远!