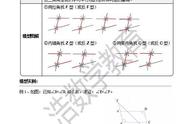
1854年黎曼更改了第五条公理,即:在一个二维平面内,不存在平行线的存在,得出了黎曼几何。黎曼几何描述的是正曲率空间的几何学,也被称为椭球几何学。
1864闵可夫斯基提出了不同以往的绝对平坦时空,称为闵式四维时空,1868年数学家贝特拉米证明的非欧几何可以在闵式四维时空的曲面上实现。

到了二十世纪初,爱因斯坦在闵式四维时空以及非欧几何的基础上提出了相对论,为人们重新塑造了整个宇宙的时空结构。
平坦的时空只不过是宇宙中小尺度上的特例,而在大尺度上不存在所谓的平坦时空,因此非欧几何才是宇宙的本质。

宇宙曲率
整个宇宙存在一定的曲率,虽然我们观察到的宇宙近似于平坦,这只能说明我们观察的尺度较小,从整个宇宙的尺度上来说,是不存在绝对的平行线,无限延长的两条线会因为宇宙的曲率相交或者发散。
因此欧式几何就像是牛顿力学,非欧几何更像是相对论。人们当时难以接受非欧几何不亚于难以接受相对论的程度。
,