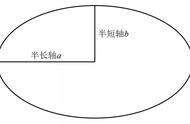
首先求半径的公式(a*a h*h)/2/h(公式中的a是半条玄长)
代入实际尺寸则为:
半径=(7888.5*7888.5 4779*4779)/2/4779=8900
求弧长的推理过程
首先正圆周长很容易了,L=(R R)× 3.14=(8.9 8.9)*3.14=55.89
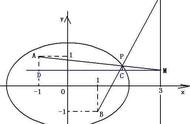
注意这个周长是整个圆的周长,我要求其中一段,就要首先虚拟一个A夹角(圆心),目前已知道这个虚拟的三角形的三条边为15777和8900和8900,根据三角形的余玄定理求出这个夹角度数
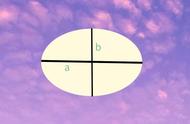
公式为:cosa=(b^2 c^2-a^2)/2bc
代入实际尺寸则为:(8.9*8.9*2-15.777*15.777)/2/8.9/8.9=-0.57
再利用计算器反余玄-0.57约等于124.75度
那么弧长=124.75/360*55.89(整圆周长)=19.37米。(面积同理)
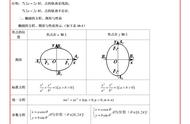
七、圆锥、圆台:

圆锥的体积=底面积×高÷3
圆锥的侧面积=S=RL÷2
(R为圆锥体底面圆的周长,L为圆锥的顶点到圆锥的底面圆周之间的距离)
解析说明:圆锥侧面展开以后就是一个扇形,扇形的弧长就是圆锥底的周长。

其实圆锥我们可能不常用到,更常用到的是圆台(比如上下不同径的圆柱)
圆台的体积公式: V=3.14×h×(R2 r2 Rr)÷3
(其中r是上底面半径,R是下底面半径)
圆台的底面和顶面近似时,圆台体积可近似为:圆台的底面面积S1加顶面面积S2除以2的平均面积1/2(S1 S2)的一个圆柱体乘以高h,即V=(S1 s2)×h÷2
圆台的侧面积公式:S=πr2 πR2 πRl πrl=π(r2 R2 Rl rl)
π=3.1415 r:上底半径、R:下底半径、h:高、l:母线=根号下[(R-r)2 h2]
(文章来源:石材匠)