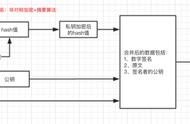
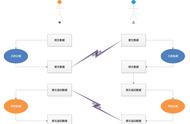
- 显然 , 对于离散对数问题 , 其正向计算得到右边 12 很简单. 但是反向运算时 , 就无从下手. 只能穷举 .
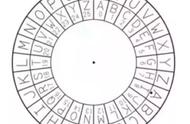
- 而且当模数使用质数 17 时 , 结果固定在 1 ~ 17 之间. 而当 17 这个模数足够大时 , 就算知道采用的是这个算法 , 也知道 17 这个质数和答案 , 想要再计算出来上图中这个问号值 , 可以想象到其难度和计算量有多大 .
2. 欧拉函数 φ
欧拉函数 :
给定任意正整数 n , 在小于等于 n 的正整数中 , 能与 n 构成互质关系的正整数个数. 复制代码
计算这个值的方式叫做欧拉函数,使用: φ(n) 表示
- 例 :chestnut::
φ(8) 有 1,3,5,7 即是 φ(8) = 4
φ(7) 有 1,2,3,4,5,6 即是 φ(8) = 6
- 问 :
那么 φ(56) 是多少 ?
先别急着一个个去数 , 我们来看下 欧拉函数的特点 .
- 当 n 是质数的时候, φ(n) = n-1
- 当 n 可以分解成两个互质的整数之积,如 n = A*B 则 : φ(A*B)=φ(A)* φ(B)
因此 :
如果 N 是两个质数 P1 和 P2 的乘积则 φ(N) = φ(P1) * φ(P2) = (P1-1)*(P2-1)
那么显然 φ(56) = φ(7) * φ(8) = 4 * 6 = 24
而 φ(63) = φ(7) * φ(9) = (7-1) * (9-1) = 48
3. 欧拉定理
如果两个正整数 m 和 n 互质,那么 m 的 φ(n) 次方减去 1 ,可以被 n 整除。

小提示: 关于定理 , 不需要我们去证明它 , 只用记住就好.
3.1 费马小定理
费马小定理 就是在欧拉定理的基础上 , 而当 n 为质数时 (φ(n)结果就是n-1 .)
那么 :
如果两个正整数 m 和 n 互质 , 且 n 是质数 ,那么 m 的 n-1 次方减去 1 ,可以被 n 整除。

4. 公式转换
- 首先根据欧拉定理

- 由于 1 的 k 次方恒等于 1 , 那么