平行四边形具有对边相等、对角相等、对角线互相平分等性质,解决某些几何题时,若能根据平行四边形的判定,巧妙地构造出平行四边形,就会化难为易、化繁为简,证明过程简捷.现举例说明。
策略1:利用平行线构造平行四边形
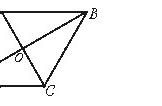
1:.点E为平行四边形ABCD中DC边的延长线上的一点,且CE=DC,连接AE分别交BC、BD于点F、G,连接AC交BD于点O,连接OF.
求证:DE=4OF.

【分析】连接BE,易证四边形ABEC是平行四边形,则AB=CD=CE,然后证明OF是△ABC的中位线,即可证得.
【解答】连接BE.∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,O是AC的中点,
∴四边形ABEC是平行四边形,∴F是BC的中点,
∴OF是△ABC的中位线,∴AB=2OF,
∵AB=CD=CE,∴DE=4OF.
2.如图,在△ABC中,E、F分别是AB、BC的中点,G、H是AC的三等分点,EG、FH的延长线相交于点D.求证:四边形ABCD是平行四边形.

【分析】连接BD交AC于O,连结BG,BH,首先证得四边形BHDG是平行四边形得到AO=OC,然后利用对角线互相平分的四边形是平行四边形判定即可.
【解答】连接BD交AC于O,连结BG,BH,
∵E是AB中点,AG=GH,∴EG是△ABH的一条中位线,
∴EG∥BH,即GD∥BH,同理可证BG∥DH,
∴四边形BHDG是平行四边形.∴BO=OD,GO=OH,
又∵AG=HC,∴AG GO=HC OH,即AO=OC,
又∵BO=OD,∴四边形ABCD是平行四边形

3.在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.若点P在BC边上(如图1),此时PD=0,可得结论:PD PE PF=AB.
请直接应用上述信息解决下列问题:
当点P分别在△ABC内(如图2),△ABC外(如图3)时,上述结论是否成立?若成立,请给予证明;若不成立,PD,PE,PF与AB之间又有怎样的数量关系,请写出你的猜想,不需要证明.