策略3:利用线段中点构造平行四边形
8.如图,在等边三角形ABC中,P为边AB上一点,Q为边AC上一点,且AP=CQ,今量得点A与线段PQ的中点M之间的距离是19cm,则点P与点C之间的距离等于_____ cm.

【分析】如图,作PN∥AC交BC于N,连接NQ,连接AN交PQ于M′.首先证明四边形APNQ是平行四边形,推出M与M′重合,再证明PC=AN即可解决问题.
【解答】如图,作PN∥AC交BC于N,连接NQ,连接AN交PQ于M′.
∵△ABC是等边三角形,∴∠B=∠ACB=60°,AB=AC,
∴∴∠PNB=∠ACB=60°,∴△PBN是等边三角形,∴PB=PN,
∵AB=AC,AP=CQ,∴PB=AQ=PN,
∴四边形APNQ是平行四边形,∴PM′=QM′,
∴M与M′重合,AM=MN=19cm,AN=38cm,
在△ABN和△CBP中,BN=BP,∠B=∠B,AB=BC,
∴△ABN≌△CBP,∴PC=AN=38cm,故答案为38cm.
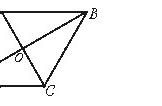
9.如图,已知四边形ABCD中,点E、F、G、H分别是AB、CD、AC、BD的中点.求证:EF和GH互相平分.

【分析】要证明EF和GH互相平分,只需构造一个平行四边形,运用平行四边形的性质:平行四边形的对角线互相平分即可证明.
【解答】证明:连接EG、GF、FH、HE,
∵点E、F、G、H分别是AB、CD、AC、BD的中点,
∴EG、HF分别是△ABC与△DBC的中位线,
∴EG=1/2BC,HF=1/2BC,∴EG=HF.
同理EH=GF.∴四边形EGFH为平行四边形.∴EF与GH互相平分.

10.如图1,P为Rt△ABC所在平面内任一点(不在直线AC上),∠ACB=90°,M为AB的中点.
操作:以PA、PC为邻边作平行四边形PADC,连接PM并延长到点E,使ME=PM,连接DE.
(1)请你猜想与线段DE有关的三个结论,并证明你的猜想;
(2)若将"Rt△ABC"改为"任意△ABC",其他条件不变,利用图2操作,并写出与线段DE有关的结论(直接写答案).