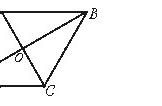
【分析】由直角三角形的性质和三角形中位线定理得出AE=1/2BC=EC,EF∥AB,EF=1/2AB,得出AD∥EF,AD=EF,证出四边形AEFD是平行四边形,得出AE=DF,即可得出结论.
【解答】DF=EC;理由如下:
连接AE,如图所示:∵∠BAC=90°,E,F分别是边BC,AC的中点,
∴AE=1/2BC=EC,EF∥AB,EF=1/2AB,
∵AD=1/2AB,∴AD∥EF,AD=EF,
∴四边形AEFD是平行四边形,∴AE=DF,∴DF=EC.

6.如图,在平行四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA上的点,且AE=CG,BF=DH,求证:EG与FH互相平分(提示:可连接EF,FG,GH,HE,证四边形EFGH为平行四边形即可).

【分析】首先连接EF,FG,GH,HE,由在平行四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA上的点,且AE=CG,BF=DH,易证得△AEH≌△CFG,即可得FG=EH,继而可得HG=EF,即可证得四边形EFGH为平行四边形,继而证得EG与FH互相平分.
【解答】证明:连接EF,FG,GH,HE,
∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D,AB=CD,AD=BC,
∵AE=CG,BF=DH,∴AH=CF,BE=DG,
在△AEH和△CFG中,AE=CG, ∠A=∠C,AH=CF,
∴△AEH≌△CGF(SAS),∴EH=GF,
同理:GH=EF,∴四边形EFGH为平行四边形,
∴EG与FH互相平分.
7.如图,在▱ABCD中,E、F分别为AC、CA延长线上的点,且CE=AF,请你探讨线段BF与DE位置及大小关系如何.

【分析】连接DF、BE、BD,BD交AC于O,根据平行四边形的性质得到OA=OC,OB=OD,进一步证出OF=OE,得到平行四边形BFDE,根据平行四边形的性质即可得到答案.
【解答】线段BF与DE位置及大小关系分别是BF∥DE,BF=DE.
理由是:连接DF、BE、BD,BD交AC于O
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵CE=AF,∴OF=OE,∴四边形BFDE是平行四边形,∴BF∥DE,BF=DE.
答:线段BF与DE位置及大小关系分别是BF∥DE,BF=DE.