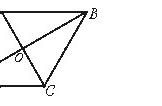
【分析】(1)连接BE,证△PMA≌△EMB,推出PA=BE,∠MPA=∠MEB,推出PA∥BE.根据平行四边形的性质得出PA∥DC,PA=DC,推出BE∥DC,BE=DC,得出平行四边形CDEB即可;
(2)连接BE,证△PMA≌△EMB,推出PA=BE,∠MPA=∠MEB,推出PA∥BE.根据平行四边形的性质得出PA∥DC,PA=DC,推出BE∥DC,BE=DC,得出平行四边形CDEB即可.
【解答】(1)DE∥BC,DE=BC,DE⊥AC,
证明:连接BE,∵M为AB中点,∴AM=MB,
在△PMA和△EMB中,PM=ME, ∠PMA=∠EMB,AM=BM,
∴△PMA≌△EMB(SAS),
∴PA=BE,∠MPA=∠MEB,∴PA∥BE.
∵四边形PADC是平行四边形,∴PA∥DC,PA=DC,
∴BE∥DC,BE=DC,∴四边形DEBC是平行四边形,
∴DE∥BC,DE=BC.
∵∠ACB=90°,∴BC⊥AC,∴DE⊥AC.

(2)解:DE∥BC,DE=BC.
,