【分析】在图2中,因为四边形PEAF为平行四边形,所以PE=AF,又三角形FDC为等腰三角形,所以FD=PF PD=FC,即PE PD PF=AC=AB,在图3中,PE=AF可证,FD=PF﹣PD=CF,即PF﹣PD PE=AC=AB.
【解答】图2结论:PD PE PF=AB.

证明:过点P作MN∥BC分别交AB,AC于M,N两点,
∵PE∥AC,PF∥AB,∴四边形AEPF是平行四边形,
∵MN∥BC,PF∥AB,∴四边形BDPM是平行四边形,
∴AE=PF,∠EPM=∠B,∠EPM=∠ANM=∠C,
∵AB=AC,∴∠B=∠C,∴∠EMP=∠EPM,∴PE=EM,
∴PE PF=AE EM=AM.
∵四边形BDPM是平行四边形,∴MB=PD.
∴PD PE PF=MB AM=AB,即PD PE PF=AB.
图3结论:PE PF﹣PD=AB.

策略2:和用相等线段构造平行四边形
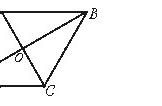
4.如图,点O是平行四边形ABCD的对角线AC与BD的交点,四边形OCDE是平行四边形.求证:OE与AD互相平分.

【分析】连接AE,根据平行四边形OCDE的对边平行且相等,得DE∥OC,DE=OC;再根据平行四边形ABCD的对角线互相平分得AO=OC,即DE∥OA,DE=OA,所以四边形ODEA是平行四边形,由平行四边形的对角线互相平分得证OE与AD互相平分.
【解答】证明:连接AE,如图.
∵四边形OCDE是平行四边形,∴DE∥OC,DE=OC
∵O是平行四边形ABCD的对角线AC与BD的交点,
∴AO=OC.∴DE∥OA,DE=OA
∴四边形ODEA是平行四边形,∴OE与AD互相平分.
5.如图,在△ABC中,∠BAC=90°,延长BA到点D,使AD=AB,E,F分别是边BC,AC的中点,试猜想DF与EC的数量关系,并证明你的猜想.