直角三角形斜边上的中线等于斜边的一半是关于直角三角形的一个定理,然而,在考试试题中往往不会直接明确地告诉你这个三角形是直角三角形或哪条线是斜边上的中线,需要你添加辅助线;而且随着我们学习的基本几何图形越来越多,这种应用不光仅仅在直角三角形中,它通常还需要结合平行四边形、棱形、正方形、双曲线、圆、抛物线等几何图形的性质。现在我们就结合几种基本几何图形来谈谈直角三角形斜边中线定理的灵活应用。

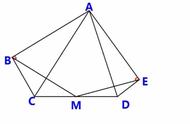
一、直角三角形斜边上的中线在三角形中的应用

二、直角三角形斜边上的中线在平行四边形中的应用
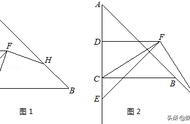
例2、如图,在▱ABCD中,∠ABC=75°,AF⊥BC于点F,AF交BD于点E,若DE=2AB,则∠AED的大小是( )
A.65° B.70° C.75° D.80°
方法:碰到某条线段长是直角三角形斜边的一半,直接添加辅助线:斜边的中线。
解:由题可知AF⊥AD,则△ADE为直角三角形
连接A与DE的中点O,易知OA=OE=OD=AB
设∠ADO=∠1
那么∠AOB=∠ABO=2∠1 ∠DBC=∠ADO=∠1
∴∠ABC=3∠1=75° ∴∠1=25°
∴∠AED=(180°-2∠1)÷2=65°

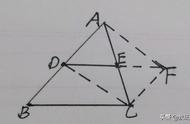
三、直角三角形斜边上的中线在正方形中的应用