巧妙数图形技巧,巧数图形的100种方法

数图形个数是小学低年级数学中经常出现的题型之一。不过很多时候，孩子由于没有掌握正确的方法，造成数数的过程中经常出错，而且消耗的时间也很多。今天就为大家介绍一种简单快捷，又不容易出错的数图形方法。

１．怎样数一条直线上线段的条数 ？

一条线上有n条独立线段，我们将它们编号为1，2，3，…，n，则这条直线上所有线段的条数是：

1＋2＋3＋…＋n

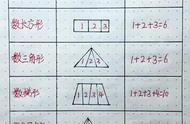
２．用数线段条数的方法，也可以数数角、三角形、长方形和立方体的个数。

例1 数出图5-1中各条线上线段的总条数。

⑴ └──┴──┴──┘

⑵ └─┴─┴─┴─┴─┴─┘

分析

⑴ 图中线上有三条独立线段，我们将这三条独立线段编上号，如图5-2：

1 2 3

└──┴──┴──┘

图5-2

现在，我们这样来数，其中

单独的线段有：⑴、⑵、⑶这三条；

由两条独立线段合并成一条线段的有：（1，2）、（2，3）这两条；

由三条独立线段合并成一条线段的有：（1，2，3）这一条。

由3＋2＋1 =6（条），我们数得图中有6条线段，他趣的是，这个得数6正是我们所编号码1、2、3这三个连续数的和。这是不是巧合呢？我们再来看⑵和⑶的结果。

⑵ 我们仿照⑴的作法将⑵图中的独立线段编上号码，如图5-3：

1 2 3 4 5 6

└─┴─┴─┴─┴─┴─┘

图5-3

单独的线段有：⑴、⑵、⑶、⑷、⑸、⑹一共6条；

两条合并成一条有：（1，2）、（2，3）、（3，4）、（4，5）、（5，6）一共5条；

三条并成一条的有：（1，2，3）、（2，3，4）、（3，4，5）、（4，5，6）一共有4条；

四条并成一条的有：（1，2，3，4）、（2，3，4，5）、（3，4，5，6）一共有3条；

五条并成一条的有：（1，2，3，4，5）、（2，3，4，5，6）一共有2条；

六条并成一条的有：（1，2，3，4，5、6）只1条。

总条数也正好是编号的六和连续数的和，即1＋2＋3＋4＋5＋6 21（条）。

说明：从上例的分析解答过程，我们可得数线段的方法，通过这种方法，我们得到一个重要的规律，这就是：单条线上线段的总条数，都等于从1开始的几个连续数的和（有几条独立线段就有几个连续数）。这样，我们就将问题由数数转化成计算，它的优点是：不重复，不漏算。

运用这种方法，我们还可数其他的图形的个数。

例2：数一数，图5-5中一共有多少个三角形？

解：将图中单独三角形1~5编号，一共有三角形是：

1＋2＋3＋4＋5 = 15（个）。

例3 图5-6中有多少个角，你会数吗？

解 将单独的角按1~7编号，可计算出共有角是：

1＋2＋3＋4＋5 ＋6＋7= 28（个）。

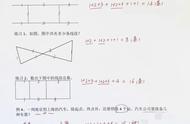
例4 数出图5-7中长方形的个数。