高尔顿
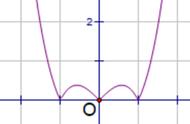
我们以4行钉板为例:如果小球要掉入最左侧或者最右侧的槽中,它必须一路顺着左边或者一路顺着右边运动,小球落入最左侧或者最右侧槽的方法数都只有1种。

但是,如果小球要运动到A的位置,就有两种方式了:要么从A的左上方向右到达A处,要么从A的右上方向左到达A处。所以,到达A处的路径数等于A左上和右上两个位置的路径数之和。A=1 1=2。
按照这个规律我们就能写出小球到达任意一个位置的方法数:等于它左上和右上两个肩膀上的数字之和。

大家看:小球到达各个位置的方法数,构成了一个杨辉三角(正如我们之前讨论过的)。而且,每次撞击钉板之后,小球向左和向右运动的概率都是1/2,因此所有的路径都是等可能的。到达某个槽的方法数越多,概率就越大。
在4行钉板时,落入槽中的方法总数有1 4 6 4 1=16种。其中落入中央槽的方法数有6种,概率就是6/16=37.5%;落入第2、4两个槽的概率是4/16=25%,而落到第1、5两个槽的概率就是1/16=6.25%。
不过,如果槽的数量增加,我们还能计算出这个概率吗?
我们来考虑一个问题:假如一共有n排钉子,对应了n 1个槽,落入第k个槽的概率有多大?根据数学计算,这个概率的表达式如下:

(1)
我们可以简单解释一下这个公式,不过如果数学不太好,也可跳过这一段,这并不影响理解本文。
因为有n排钉子,小球每次撞击钉子有2种选择,所以最终小球的路径方法数有2^n种。如果想要落入第k个槽,那么在n次与钉子的撞击中,需要有k-1次落到钉子右侧,n-k 1次落到钉子左侧。因此我们从n次碰撞中选择出k-1次向右运动,方法就是组合数C(n,k-1)种。用落入该槽的方法数,除以一共的方法数,就得到了概率。
仔细观察这个表达式,我们会发现:假如要计算n=100时落入各个槽的概率,就需要计算到100的阶乘,即