高中数学|求圆的方程常见方法总结与归纳,拓展思维还得看后两种
圆的方程在习过程当中,我们要对圆的定义有充分的理解,结合图形才能明白其表达的实际意义。原是指平面上到定点的距离等于定长的点的集合,其定点是圆心,定长是圆的半径。由此而推导出来的圆的标准方程,即定点和圆心两点之间的距离等于半径。圆的方程一般分为标准方程和一般方程。

而圆的一般方程则是将圆的标准方程展开之后所得到的二元二次方程,一般方程当中含有三个待定的字母,也即在求解圆的一般方程过程当中,只要已知三个独立的条件,就可以求解圆的一般方程。从圆的一般方程可以看出其最基本的条件及二次(平方项)项系数相等,且不等于0。Xy乘积得项不存在,即其系数为0。外外一次向系数的平方和减去四倍的常数项大于0。通过以上的三个条件就可以判定。一个二元二次方程是否表示圆。

那么在球员的方程过程当中,我们常见的有以下四个方法:
第一,直接代入法,已知圆心坐标和半径大小,直接带入圆的标准方程即可求解,这种方式是比较简单的。
第二,待定系数法主要是根据题目中的条件设出所求圆的标准方程或者是一般方程。然后根据已知的条件建立圆心坐标和半径的方程组。最后将方程解出,求出圆心坐标和半径的值,并把它们带入所说的方程当中,就可以得所求圆的方程。而对于一般方程而言,则是建立有关于一次项系数和常数项为未知数的方程组。

第三,几何性质法如果在求解圆的方程时,能够结合原有关的几何性质来进行考察,可以使思路更加的直观,计算简单,这就是我们说的利用数形结合的思想来进行解题。而在利用几何性质来求解圆的方程式,常用的几何性质有:
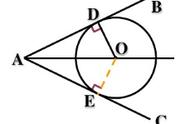
一,圆心到切点的连线垂直一过切点的圆的切线。
二,圆心到切线的距离等于半径。
三,圆的半径,半弦长,弦心距构成直角三角形。
四,圆中任意弦的垂直平分线,必过圆心。
五,圆内的任意两条弦的垂直平分线的交点一定是圆心。
以上的这几条性质都是利用几何法来进求圆方程式能用到的重要性质,也是我们在解题时解题思路形成的突破口。
第四,定义法,这种方法要先判断轨迹是圆,然后再写出方程。也就是利用两点之间的距离是否等于半径的关系作为判断的标准。