然而在具体求原方程的过程当中,如何根据实际的情况来进行解题,以下的三个方法是非常不错的。
一,如果有已知条件,容易求出圆心坐标半径或方便利用圆心的坐标和半径列方程,一般采用圆的标准方程进行求解,再用待定系数法求出圆心和半径的值即可。
二,如果已知条件和圆心或半径都无直接的关系,一般采用圆的一般方程,再用待定系数法求出各个字母的值。

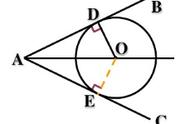
三,注意圆的性质的应用,比如垂径定理,切线,直角三角形等性质的应用,要注意适时地运用几何知识来列方程,这样可大大减少运算量。而且在具体的题型考察当中,一般中等难度以及偏难的题型都更多地加入了圆的性质。所以对于几何性质法的运用,在求圆的方程过程当中是极为重要的,也即对数形结合方法的运用,能更多地考察同学们对圆的性质以及圆的代数方程的综合。

另外,在求圆方程学习的过程当中,很多同学提到如何来判断四点是否共圆,其实就是和求圆方程的方法比较类似,主要多出一个步骤而已,首先我们可以将四点中的3点来确定圆的方程,也即可直接利用待定系数法求出圆的方程,然后再将第4点带入方程当中,看其是否满足圆的方程,如果满足则4点共圆,不满足则4点不共圆即可,这属于求圆的方程的实际应用。

写在最后,有关圆的方程的求解,除了对圆的两种方程的形式,利用待定系数法,可直接带入法进行求解以外,对于几何性质法的运用也是大家学习中的重点。利用圆的性质和圆的代数方程相结合的方法将是中等题型当中考察的重点,也是大家进行思维拓展的最好方式,其难度并不是很大,只需要将以前学习的有关圆的兴致在图形当中进行全面的梳理,然后配合元芳城的性质来进行求解即可。