式中,μ为基本模型计算的摩擦系数;vo为当前轧制过程中轧制速度,m/min;ε为当前轧制道次的压下率;nr为当前使用的工作辊轧制的钢卷数;μ0、μ1、μ2、μ3、μ4、μ5为计算摩擦系数模型当中的系数。
2.4张力影响悉数模型
冷轧生产过程是在一定前张力和后张力的作用下实现的,在轧制力计算过程中,前后张力通过对轧件的变形抗力的影响进而影响轧制力的计算。

式中,te为张力影响系数;tb为轧件的单位后张力,N/mm2;tf:轧件的出口单位张力,N/mm2;sk:轧件的动态变形抗力,N/mm2。
3 模型参数优化
对于二十辊轧机轧制力模型优化的方法有如下两种:自学习系数在线自学习和根据现场数据模型参数离线优化。
3.1 轧制力自学习
由于所采用的Bland-Ford-Hill轧制力模型是在一定假设条件下建立的,计算的结果跟实际的情况会有一定的差距,因而采用自学习的方法对轧制力结果进行修正。在当前钢卷轧制结束以后采用的是指数平滑的自学习方法计算新的自学习系数,使其能够更准确地修正计算的轧制力,以用于下一个钢卷的计算[5-7]。具体的计算步骤如下:
1. (1)根据现场采集的实际数据(包括原料厚度、带钢的道次出入口厚度、带钢宽度、轧辊半径、前后张力等数据)在自学习系数取1时,调用Bland-Ford-Hill轧制力模型计算轧制力P1;
2. (2)由现场采集的实际轧制力P2与轧制力P1相除计算出新的自学习系数;
3. (3)使用当前钢卷使用的自学习系数ZP1和实际值反算的自学习系数ZP2采用指数平滑法(如式21)计算新的自学习系数ZP[5]。

式中,△为增益系数,在这里取0.5。
3.2轧制力模型系数优化
轧制过程非常复杂,很难通过模拟实验的方法对轧制模型当中的模型参数进行优化,只能通过采用现场数据,离线对其进行优化。在使用的轧制力模型当中可以进行优化的参数有:变形抗力计算模型当中的I、m、n和摩擦系数计算模型当中的μ0、μ1、μ2、μ3、μ4、μ5。可以通过调整模型当中的这些参数,使模型计算的轧制力与轧制过程当中的实际轧制力的吻合程度更高。具体的优化方法如下:
(1)从现场采集大量的同一钢种在轧制过程中实际的原料厚度、带钢的道次出入口厚度、带钢宽度、轧辊半径、前后张力、轧制速度、轧制力等数据。
(2)对采集的每一组数据,使用前面介绍的轧制力模型在自学习系数为1的情况下,计算每一组的轧制力。
(3)计算每一组数据中的实际轧制力与计算的轧制力的比值,即在模型当中应当使用的自学习系数。
(4)调整变形抗力计算模型当中的、、和摩擦系数计算模型当中的μ0、μ1、μ2、μ3、μ4、μ5,并重复步骤2和3,对所有的带钢实际数据计算应当使用的自学习系数。
(5)直至所有的自学习系数落在0.9~1.1之间并且使轧制力的自学习系数尽可能地靠近1时,停止对变形抗力计算模型当中的、、和摩擦系数计算模型当中的μ0、μ1、μ2、μ3、μ4、μ5值的调整,如图2所示。

图2 模型优化效果图
图2显示了调试的结果,显示了随着压下率的变化和轧制速度的变化自学习系数的分布规律,以及轧制力自学习系数的分布符合标准正态分布。
3.3轧制力模型优化应用实例
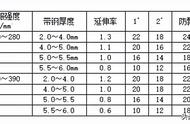
表1显示了模型优化前和模型优化后在自学习系数为1时,模型计算的轧制力、实际轧制力、计算的自学习系数、偏差值的对比。
从表中可以看出,在轧制力模型参数优化前后,轧制力的预报精度有了大幅度提高,所有道次的轧制力的预报偏差都在2%以内,甚至在最后1个道次,预报偏差只有0.01%。
4 总结
1. 本文介绍了单机架可逆二十辊森基米尔轧机的平面布置,给出了计算二十辊森基米尔轧机的轧制力模型,并对模型进行了分析。给出了轧制力模型当中摩擦系数、变形抗力等重要因素的计算方法。采用指数平滑法对二十辊森基米尔轧机的轧制力模型进行自学习。给出了二十辊森基米尔轧机模型参数的优化方法,并将参数优化前后进行了对比。实践证明该轧制力模型可以给出非常精确的二十辊森基米尔轧机的轧制力设定值。同时,给出的模型优化方法和自学习方法,使得该模型在复杂工况条件下具有较强的适应能力。
参考文献:
[1]潘纯久.二十辊轧机及高精度冷轧带钢生产[M].北京:冶金工业出版社,2007.
[2]李慧芳,郭 花.20辊森吉米尔轧机辊系结构分析[J].应用技术,1999,(1):60-61.
[3]王彦廷.ZR-33WF-18″20辊森吉米尔轧机技术[J].冶金设备,2000,(5):34-38.
[4]方胜年.森吉米尔20辊轧机的新技术[J].电工钢, 2002,(2):16-17.
[5]刘相华,胡贤磊,杜林秀,等.轧制参数计算模型及其应用[M].北京:化学工业出版社,2007.
[6]杨 节.轧制过程数学模型[M].北京:冶金工业出版社,1993.
[7]孙一康.冷热轧板带轧机的模型与控制[M]. 北京:冶金工业出版社,2010.
,