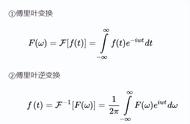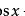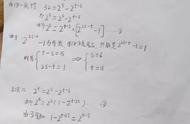数论有什么用途,数论解决什么问题

，在给定圆的所有内接（外切）n边形中，以正n边形的面积最大（小）。（也许值得补充的是，对单位圆（半径为1的圆），当 n趋向无穷大时，正 n边形的面积就趋向于单位圆的面积π，这就是古代数学家求圆周率的近似值的方法“穷竭法”。）

4.不可公度量之线段与无理数

这一篇回到数。 对古希腊人来说，从自然数过渡到整数，进一步从整数扩充到分数（正分数作为自然数的比值），这都是比较容易理解的。然而，当他们发现存在着不能用两个整数之比表示的比值，比如单位正方形的对角线长与边长之比

时，其惊讶可想而知！ 的无理性的证明，揭开了古希腊数学中辉煌的一页：实数理论。从现在的眼光看，古希腊人其实非常理性，因为他们终究接受了 ，虽然将它归为“无理数”这一类。

5.垂足三角形的极小值性质 与 6.极小值性质的第二个证明

这是几何学中著名的 Fagnano’s Problem： 在一个给定的锐角三角形中，求所有内接三角形中具有最短周长的那一个。意大利数学家 GiovanniFagnano 在 1775 年首先提出并用微积分解决了这一问题，答案是所谓的垂足三角形，即给定锐角三角形的三个垂足所连接而得到的三角形。第5和第6节，分别给出了属于德国数学家 H. Schwarz 和匈牙利数学家 L. Féjer 的初等证明。 Féjer 是 Schwarz 最得意的学生，在学生时代发现了这个更简单的证明而引起老师的重视。

via：林开亮老师(西北农林科技大学)

回复：数学欣赏

获取《数学欣赏》电子版

微信ID：超级数学建模（supermodeling）

数模君已和太白山果农联合推出数模君水果铺！！

只推当季水果，欢迎各位品尝！

,