微积分是现代科学的基础,学习微积分是一个现代人的必修课。
数学在于给出有效的计算方法,并且要解释它为什么有效。比如已知一个直角三角形的两个直角边的长度,我们可以依据勾股定理(勾股定理的发现是长期经验积累的一次创新),计算出斜边的长度,同时,还需要以可理解的方式证明勾股定理,给出其适用的条件。这样,我们的认知才是圆满的,我们看到的世界才不是现象或概念的混合,而是有层次有秩序的运行着的。
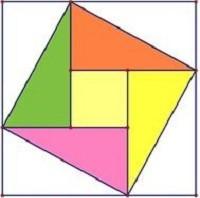
图1 勾股定理的证明
微积分的发明也是这样,对于求运动速度,求曲线切线,求曲线长度、所围面积、立体体积,求极大值和极小值等问题,我们可以依据求微分,求导数,求积分的原则进行计算。但要论证它为什么是正确的,就不如勾股定理那样的容易了。
我们以求运动速度为例1,求曲线所围面积为例2来简要介绍微积分的方法。