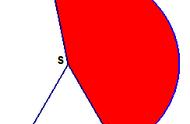
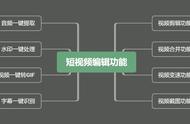
三棱柱ABC-A'B'C'的底面积(即△ABC的面积)为s,高(即点A'到平面ABC的距离)为h,则它的体积为sh,沿平面A'BC和平面A'B'C,将这个三棱柱分割为3个三棱锥,其中三棱锥1,2的底面积相等(S△A'AB=S△A'B'B),高也相等(点C到平面ABB'A'的距离);三棱锥2,3也有相等的底面积(S△B'BC=S△B'C'C)和相等的高(点A'到平面BCC'B'的距离)。因此,这三个三棱锥的体积相等,每个三锥的体积等于等底等高三棱柱体积的1/3。

这样进一步推广,不光是棱锥体,圆锥也一样。只要是锥体,等底等高的锥体体积都相等。这样很容易由等积关系看出,所有锥体的体积都等于与它等底等高柱体体积的1/3。

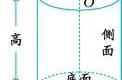
最后,回到最初圆柱圆锥的分割图上,由于圆柱分割成许多近似的小三棱柱,圆锥分割成对应的许多小三棱锥,每一小块小三棱锥的体积都是对应小三棱柱体积的三分之一,因此最终的圆锥体积是等底等高的圆柱体积的三分之一。这个中学生可以完全理解,小学生理解力好的其实也能理解。

好了,最后希望这些内容可以帮助我们的孩子提高数学学习的兴趣和热情,更多的数学问题,大家可以在下方留言,我们一起来研究吧!
,