学习目标2 3.通过计 算四种平 面图形的 面积,明确
的 意义。突破 难点和易 错点,让模 糊的知识 清晰化。感 悟“转化” 的数学思 想。
学生活动2
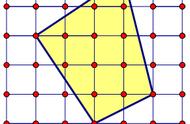
- 学生数一数,算一算这四个图形的面 积。
- 明确梯形和三角形面积公式中92 的含义。
生1:如果不:2,算的就是两个这样 的梯形或三角形的面积了。
教师指导2
师:看下边这四个图形,
有什么想说的么?
质疑:梯形、三角形 的面积公式中都有:
2,为什么92后面积
还相等?不除以2算
的是谁的面积?
学习评价2
1.会交流,敢 表达,有理有 据( 1)
2.能正确计 算平面图形 的面积,计算 正确,表达严 谨( 1)
三、补缺,让已有的知识活化
学习目标3 | 学生活动3 | 教师指导3 | 学习评价3 |
4.经历用 以盈补虚 法推导三 角形面积 的过程,理 解计算组 合图形的 多种算法, 并能正确 | 1.生:它的顶点一格一格的向右平移, 形状变了,面积没变。 | 1.师:这个直角三角 形是如何变化的?变 化过程中,什么变了? 什么没变? |
灵活的运 用公式进 行计算,发 展空间观 念。
2.图中深色的三角形 形状相同么?面积 呢?
- 比较两个三角形面积的大小。
3.直角三角形想通过 不同的变化,使面积 保持不变,你们能帮 帮直角三角三角形 吗?
- 还可以变成底6格、高4格 还可以变成底8格、高3格 还可以变成底12格、高2格 .....
只要底与高的乘积不变,面积就不变。 解决易错题训练
- 面积相等的两个三角形一定等底
等高吗?
4.引导学生从新的视 角理解面积。
- 两个等底等高的三角形,它们的
形状一定相同吗?
- 从新认识“面积”
1.理解以盈补

面积
• •
15
长度
虚,会用
“割”、“补”
的方法解题,计
算正确( 1)
2.思路严谨、表
达准确( 1)


5.生分组研究用一个三角形转化成长
方形,并尝试推导三角形的面积公式。
K方形的成枳 =K X 宽
II II II
为形的ihi砍=成X〈样寻2)
师:同学们可真 聪明,想到了古 代数学家想到 的方法。
5师:直角三角形是 怎样变化的?在变化 过程中,什么变了? 什么没变?
师:你能根据这个转 化过程推导三角形的 面积公式吗?