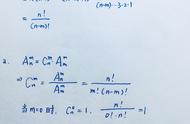①从n个不同元素中取出m个元素后就剩下n-m个元素,因此从n个不同元素中取出 n-m个元素的方法是一一对应的,因此是一样多的就是说从n个不同元素中取出n-m个元素的唯一的一个组合.
(或者从n 1个编号不同的小球中,n个白球一个红球,任取m个不同小球其不同选法,分二类,一类是含红球选法有

一类是不含红球的选法有Cn的m次方)
②根据组合定义与加法原理得;在确定n 1个不同元素中取m个元素方法时,对于某一元素,只存在取与不取两种可能,如果取这一元素,则需从剩下的n个元素中再取m-1个元素,所以有Cn的(m-1)次方,如果不取这一元素,则需从剩余n个元素中取出m个元素,所以共有cn的m次方种,依分类原理有Cn的(m-1)次方 Cn的m次方=C(n 1)的m次方.
⑷排列与组合的联系与区别.
*都是从n个不同元素中取出m个元素.
区别:前者是“排成一排”,后者是“并成一组”,前者有顺序关系,后者无顺序关系.
⑸①几个常用组合数公式


②常用的证明组合等式方法例.
i. 裂项求和法. 如:1/2! 2/3! 3/4! ... n/(n 1)!=1-1/(n 1)!(利用(n-1)/n!=1/(n-1)!-1/n!)
ii. 导数法.
iii. 数学归纳法.
iv. 倒序求和法.
v. 递推法(即用Cn的m次方 Cn的m-1次方=C(n 1)的m次方递推)如: