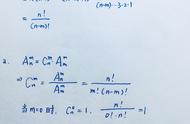vi. 构造二项式. 如:

证明:这里构造二项式(x 1)ⁿ(1 x)ⁿ=(1 x)²ⁿ其中xⁿ的系数,左边为

而右边为C₂n的n次方
四、排列、组合综合.
1. I. 排列、组合问题几大解题方法及题型:
①直接法. ②排除法.
③捆绑法:在特定要求的条件下,将几个相关元素当作一个元素来考虑,待整体排好之后再考虑它们“局部”的排列.它主要用于解决“元素相邻问题”,例如,一般地,n个不同元素排成一列,要求其中某m(m≤n)个元素必相邻的排列有A(n-m 1)的(n-m 1)次方·Am的m次方个.其中A(n-m 1)的(n-m 1)次方是一个“整体排列”,而Am的m次方则是“局部排列”.
又例如①有n个不同座位,A、B两个不能相邻,则有排列法种数为An的平方-A(n-1)的1次方·A₂².
②有n件不同商品,若其中A、B排在一起有A(n-1)的(n-1)次方·A₂².
③有n件不同商品,若其中有二件要排在一起有An的平方·A(n-1)的(n-1)次方.
注:①③区别在于①是确定的座位,有A₂²种;而③的商品地位相同,是从n件不同商品任取的2个,有不确定性.
④插空法:先把一般元素排列好,然后把待定元素插排在它们之间或两端的空档中,此法主要解决“元素不相邻问题”.
例如:n个元素全排列,其中m个元素互不相邻,不同的排法种数为多少?A(n-m)的(n-m)次方(插空法),当n – m 1≥m, 即m≤(n 1)/2时有意义.
⑤占位法:从元素的特殊性上讲,对问题中的特殊元素应优先排列,然后再排其他一般元素;从位置的特殊性上讲,对问题中的特殊位置应优先考虑,然后再排其他剩余位置.即采用“先特殊后一般”的解题原则.
⑥调序法:当某些元素次序一定时,可用此法.解题方法是:先将n个元素进行全排列有An的n次方种,m(m<n)个元素的全排列有Am的m次方种,由于要求m个元素次序一定,因此只能取其中的某一种排法,可以利用除法起到去调序的作用,即若n个元素排成一列,其中m个元素次序一定,共有An的n次方/Am的m次方种排列方法.
例如:n个元素全排列,其中m个元素顺序不变,共有多少种不同的排法?
解法一:(逐步插空法)(m 1)(m 2)…n = n!/ m!;解法二:(比例分配法)An的n次方/Am的m次方.
⑦平均法:若把kn个不同元素平均分成k组,每组n个,共有

例如:从1,2,3,4中任取2个元素将其平均分成2组有几种分法?有C4的平方/2!=3(平均分组就用不着管组与组之间的顺序问题了)又例如将200名运动员平均分成两组,其中两名种子选手必在一组的概率是多少?