图2:牛津大学物理学家,David Deutsch。
牛津大学的物理学家David Deutsch[2]多年来一直在寻求避免这种困境,他提出了一种理论,即(正如他所说)“物理过程中并没有概率和随机性的世界”。他的项目,现在正在和Marletto合作,被称为构造子理论(constructor theory)。它的目的不仅是确定哪些过程可能发生和不可能发生,而且确定哪些过程是可能的,哪些是完全不可能的。
构造子理论旨在用关于可能和不可能转换的陈述来表达所有物理学。它与热力学开始的方式相呼应,因为它将世界的变化视为以循环方式工作的“机器”(构造函数)产生的东西,遵循著名的卡诺循环的运行模式,它在19世纪用于描述发动机如何工作。构造函数就像一个催化剂,促进一个过程,并在最后恢复到原来的状态。
“假设你有一个转变,比如用砖头盖房子,”Marletto说。“你可以想出许多不同的机器来实现这一点,并达到不同的精度。所有这些机器都是构造器,在一个循环中工作”——当房子建造完成时,机器会恢复到原来的状态。
但仅仅因为执行某项任务的机器可能存在,并不意味该任务可以被撤销。建造房屋的机器可能无法拆除它。这使得构造函数的操作不同于描述砖块运动的动力学定律,其中后者是可逆的。
Marletto说,这种不可逆性的原因在于,对于大多数复杂的任务,构造函数都适合给定的环境。它需要来自与该任务相关的环境中的一些特定信息。但反向任务将从不同的环境开始,因此相同的构造函数不一定能工作,“这台机器只能适用于它工作的环境,”她说。
最近,Marletto与牛津大学的量子理论家Vlatko Vedral[3]及其在意大利的同事合作,表明构造子理论确实确定了在这个意义上不可逆的过程——即使一切都根据本身完全可逆的量子力学定律发生。“我们展示了一些转换,你可以找到一个方向的构造函数,但不能找到另一个方向的,”她说。
研究人员考虑了一种涉及量子比特 (qubits) 状态的转换,它可以存在于两种状态中的一种或两种状态的组合或叠加中。在他们的模型中,当单个量子位B与其他量子位相互作用时,它可能会从某个初始的和已知的状态B1转换为目标状态B2,一次移动一个量子位。这种相互作用使量子比特纠缠在一起:它们的属性变得相互依赖,因此除非你同时查看所有其他量子比特,否则你无法完全表征其中一个量子比特。
Marletto说,随着行中的量子比特数量变得非常大,可以根据需要将B带入状态B2。B与量子比特行的顺序交互过程构成了一个类似构造函数的机器,将B1转换为B2。原则上,你也可以撤消该过程,将 B2转回B1,方法是将B沿行送回。
但是,如果在完成一次转换后,你尝试使用新的B将量子比特数组重用于相同的过程怎么办?Marletto及其同事证明,如果行中的量子比特数量不是很大,并且你重复使用同一行,则阵列变得越来越无法产生从B1到B2的转换。但至关重要的是,该理论还预测,该行变得更不能进行从B2到B1的反向转换。研究人员通过使用B的光子和光纤电路来模拟一排三个量子比特,并通过实验证实了上述预测。
“你可以在一个方向上任意逼近构造函数,但在另一个方向上不行,”Marletto说。转换存在非对称性,就像第二定律的那样。这是因为转换将系统从所谓的纯量子态 (B1) 转变为混合态 (B2,与行纠缠)。一种纯粹的状态是我们对它了解的一切都知道的状态。但是当两个物体纠缠在一起时,你不能完全指定其中一个而不知道另一个。事实是,从纯量子态到混合态比反之更容易——因为纯态的信息通过纠缠散布,很难恢复。这就好比一滴墨水分散在水中后试图重新形成墨水,这是第二定律施加的不可逆过程。
因此,这里的不可逆性“只是系统动力学演化方式的结果,”Marletto说。它没有统计方面的内容。不可逆性不仅是最可能的结果,而且是不可避免的结果,由组分的量子相互作用决定。“我们的猜想是,”Marletto说,“热力学不可逆性可能源于此。”
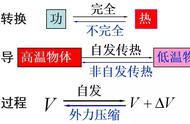
不过,还有另一种思考第二定律的方式,它首先由苏格兰科学家詹姆斯·克拉克·麦克斯韦(James Clerk Maxwell)设计,他与玻尔兹曼创立了热力学的统计观点,麦克斯韦当时并没有意识到这一点,但他将热力学定律与信息问题联系起来。
麦克斯韦对宇宙热寂论和似乎破坏自由意志的无情变化规则的神学含义感到困扰。所以,在1867年,他想方设法在第二定律中“挖洞”。在他的假设场景中,一个微观生物(后来,令他烦恼的是,被称为妖精)将“无用”的热量重新转化为做功资源。麦克斯韦先前已经证明,在热平衡的气体中存在分子能量分布。有些分子比其他分子“更热”——它们运动得更快,能量也更多。但它们都是随机混合的,所以人们似乎没有办法利用这些差异。
进入麦克斯韦妖[4]。它将气体隔间一分为二,然后在它们之间安装一个无摩擦的活板门。恶魔让在隔间周围移动的较热分子沿一个方向通过活板门,但不能反向通过。最终,恶魔的一侧有热气,另一侧有冷气,它可以利用温度梯度来驱动某些机器。
麦克斯韦妖利用分子运动的信息破坏了第二定律。因此,信息是一种资源,就像一桶石油一样,可以用来作功。但由于这些信息在宏观尺度上对我们隐藏,我们不能利用它。正是因为不知道微观状态的具体形式迫使经典热力学谈论平均值和集合。
近一个世纪后,物理学家证明麦克斯韦妖从长远来看不会颠覆第二定律,因为它收集的信息必须存储在一个地方,任何有限的记忆最终都必须被抹去,以便为更多信息腾出空间。1961 年,物理学家Rolf Landauer证明,如果不消耗最少值的热量,就永远无法完成信息的擦除,因此信息擦除过程提高了周围环境的熵。所以第二定律只是推迟了,而不是被打破了。
第二定律的信息视角现在被重新定义为一个量子问题。这是因为人们认为量子力学是一种更基本的描述——麦克斯韦妖本质上将气体粒子视为经典的球。但它也反映了人们对量子信息论的兴趣。我们可以使用经典无法做到的量子原理来处理信息。特别是,粒子的纠缠使信息能够以非经典方式传播和操纵。
至关重要的是,量子信息论提出了一种摆脱困扰热力学经典观点的麻烦的统计图景的方法,在这种情况下,你必须对许多不同的微观状态的集合取平均值。卡尔加里大学的Carlo Maria Scandolo[5]说:“量子信息论的真正新颖之处在于人们可以用与环境的纠缠来代替整体。”

图3:卡尔加里大学的物理学家Carlo Maria Scandolo。
他说,在集合中使用资源反映了这样一个事实,即我们只有部分关于状态的信息——可能是这个微观态,也可能是其他的微观态,它们具有不同的概率。在这种情况下,我们必须对概率分布进行平均。但是量子理论提供了另一种产生部分态的方法:通过纠缠。当一个量子系统与它的环境纠缠在一起时,我们不可能知道所有关于这个系统的信息,一些关于这个系统本身的信息不可避免地会丢失:它最终处于一个混合状态,在这个状态下,即使只关注这个系统,你也无法从原则上了解它的所有信息。
然后人们不得不用概率来描述,这不是因为你无从知晓这个系统的某些信息,而是因为其中一些信息在根本上是不可知的。Scandolo说,使用这种方式,“纠缠自然会产生概率”,“只有在存在纠缠的情况下,通过考虑环境的作用来获得热力学行为的整个想法才有效。”
这些想法现在已经变得非常精确。Scandolo与香港大学的Giulio Chiribella[6]合作,提出了量子信息的四条公理,这四条公理是获得“显性热力学(sensible thermodynamics)”所必需的,即一条不基于概率的公理。这些公理描述了与环境纠缠在一起的量子系统中信息的约束。特别是,在系统和环境中发生的一切在原则上是可逆的,这就像量子系统如何随时间演化的标准数学公式所描述的那样。

图4:香港大学的物理学家Giulio Chiribella。
Scandolo和Chiribella证明,由于这些公理,无关系统会通过可逆的相互作用变得更加相关。关联是连接纠缠物体的概念:一个物体的属性与另一个物体的属性相关。它们是通过“互信息(mutual information)”来衡量的,这是一个与熵相关的量。因此,相关性如何改变的约束也是熵的约束。如果系统的熵减少,则环境的熵必须增加,使两个熵之和只能增加或保持不变,但决不能减少。Scandolo说,通过这种方式,他们的方法从基本公理推导出熵的存在,而不是从一开始就假设它存在。
想要理解这个新的量子热力学版本,最通用的方法之一是使用资源理论,它再次谈到哪些转换是可能的,哪些是不可能的。“资源理论是一个简单模型,适用于任何情况,在这种情况下,你可以执行的动作和可以访问的系统由于某种原因受到限制,”美国国家标准与技术研究院的物理学家Nicole Yunger Halpern[7]说。(Scandolo也将资源理论融入了他的工作中)
量子资源理论采用了量子信息论所提出的物理世界的图景,在这个图景中,物理过程是可能的,存在着根本的局限性。在量子信息理论中,这些局限性通常表示为“不可行定理”:声明说“你做不到!”例如,从根本上讲,复制未知量子态是不可能的,这一想法被称为量子不可克隆(quantum nocloning)。
资源理论有几个主要成分,允许的操作称为自由操作。“一旦你指定了自由操作,你就定义了理论——然后你可以开始推理哪些转换是可能的或不可能的,并询问我们可以执行这些任务的最佳效率是什么,”Yunger Halpern说。同时,一种资源的定义是,一个热源可以用来做一些有用的事情的东西——它可以是一堆煤,来点燃炉子和驱动蒸汽机。也可能是额外的记忆,让麦克斯韦妖在更长的时间内颠覆第二定律。
量子资源理论允许放大经典的热力学第二定律的精细细节。人们不需要考虑大量的粒子;可以在其中的几个中说明什么行为是允许的。Yunger Halpern说,当我们这样做时,经典的第二定律(最终熵必须等于或大于初始熵)只是各种不等式关系的粗粒度总和。例如,经典的第二定律认为,人们可以把一个非平衡状态转化成一个更接近热平衡的状态。但“调查这些状态中哪一个更接近热平衡态并不是一个简单的问题,”Yunger Halpern说。为了回答这个问题,“我们必须检查一大堆不等式。”

图5:美国国家标准与技术研究院的物理学家Nicole Yunger Halpern。
换句话说,在资源理论中,似乎有一大堆的迷你第二定律。“因此,可能存在一些传统第二定律允许的转换,但被更细致的非平衡集合所禁止,”Yunger Halpern说。因此,她补充道:“有时我觉得这个领域的每个人都有自己的第二定律。”
维也纳大学的物理学家Markus Müller[8]说,资源理论方法“承认热力学定律等在数学上完全严格的推导,没有任何概念或数学上的松散部分。”他说,这种方法涉及“重新思考热力学的真正意义”。与其说是关于运动粒子的大集合的平均属性,不如说是关于一个热源与自然抗衡的游戏,以利用可用资源有效地执行任务。不过,最终的关键还是信息。Yunger Halpern说,丢弃信息——或无法跟踪信息——确实是第二定律成立的原因。
这些重建热力学和第二定律的努力让人想起了德国数学家David Hilbert提出的问题。1900年,他提出了23个他希望解决的数学中悬而未决的问题。该清单中的第六个问题是“用公理来处理今天那些数学在其中已经发挥重要作用的物理科学。”希尔伯特担心,他那个时代的物理学似乎建立在相当武断的假设之上,他希望这些假设能变得更严格,就像数学家尝试推导基本公理一样。