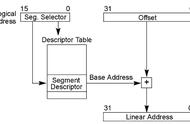
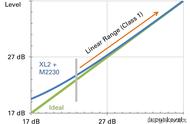
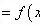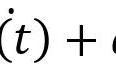我们经常听到线性代数、线性时不变、线性方程组等等,其实这几个线性都说的是一回事,都翻译为linear。
那线性到底是什么意思呢?
几何定义:直和弯的区别。
若某数量关系的函数图像呈现为一条直线或线段,那么这种关系就是一种线性关系。
比如,y=kx b,就是“线”性。
比如,y=x^2=x*x,就不是线性,它是“弯”的。
更本质的是代数定义:如果一种运算同时满足特定的“加性”和“一次齐性”,则称这种运算是线性的。
加性:L(x t)=L(x) L(t)
一次齐性:L(mx)=mL(x)
比如说,如果,你带3块钱走进一个房间,出房间后钱变成了6块;
然后你带4块钱走进这个房间,出房间后钱变成了8块;
你带n块钱走进这个房间,出来钱就变成了2n块;那么,这个房间(系统)就具有“一次齐性”。
如果你再带3 4=7块钱走进这个房间,出房间后钱变成了14块;那么,这个房间(系统)就具有“加性”。
同时满足“加性”和“一次齐性”,则称这个系统是线性的。
线性系统也就是:输入增加多少倍,输出就增加多少倍;若干次输入加起来一同送入系统的输出,等于将若干次输入分别送入系统的若干个输出相加。
数学中,有线性微分方程的说法,其实也是这个意思。
如果描述某个系统的方程其输入(自变量x)增加多少倍,输出(因变量y)也增加多少倍,则称它为线性微分方程,当然,这个系统称为线性系统。
重点注意,线性系统的冲激响应,或者阶跃响应,或者由其它激励产生的响应,不一定是直线,完全可以是曲线。
线性指的是:冲激强度(输入)增大两倍,相应的响应也会随着增大两倍。它描述的是输入和输出之间的影响关系,而不是说输出本身是神马样子。
系统输出是不是直线,微分方程的y解出来是不是直线,根本不是关键。
,