2.计算结果E<1
此时当自变量X变动1%时,因变量Y的变动小于1%,所以我们说Y对于X不够敏感;

3.计算结果E=1
此时存在一个X’,Y的任何数据都在X’的情况下成立,除此之外Y均不成立。我们说Y对X是完全弹性。

4.Y的数值和X的变化没有任何关系
不论X如何变化,Y的数值永远等于Y’,我们称之为Y对X无弹性。

理论就不进一步展开了,我们知道弹性有4种可能性即可。
另外,弹性理论的优点在于:不用考虑到X和Y是不同单位的数字,因为是比例关系的可以方便比较两者之间的关系。
二、项目中的弹性
我们回到项目的案例,假设决定总工作量的因素有单位需求工作量X和需求数量Y。当单位需求工作量X发生变化时,需求数量Y也会发生变化,因为随着需求难度的提升,项目能完成的需求数量必然会减少。
假设二者之间有函数关系:F(X)=Y。那么回到文章一开始提出的问题:
项目在规划的时候,怎么去衡量难度高的研发任务和难度低的研发任务各自的资源投入量,以达到最佳的效率(即最高的项目产出)?
1.弹性>1
对于一些难度大的工作,完成时间会成倍增加,进而导致了最终需求的数量大比例的减少。换句话说,需求数量Y的变化对需求完成的难度——即单位需求完成时间X的变化更加敏感,在这种情况下,
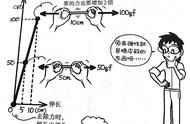
如下图所示:
- 增加1%的单位工作量(即从X2变成X1),完成时间的减少比例(即从Y2变成Y1)大于1%。
- 减少1%的单位工作量(即从X1变成X2),完成时间的增加比例(即从Y1变成Y2)也大于1%。